.Problema para ajudar na escola: Um reservatório d’água

Problema
(A partir do 2º ano do E. M.- Nível de dificuldade: Fácil)

---

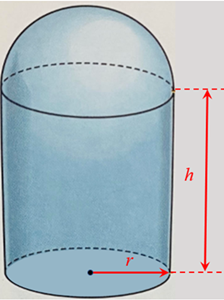
Um reservatório de água de um laboratório foi montado acoplando-se a um cilindro circular reto uma semiesfera de mesmo raio.
(a) Expresse o volume [tex]V[/tex] do reservatório em função do raio [tex]r[/tex] e da altura [tex]h[/tex] do cilindro.
(b) Supondo que a altura do cilindro é igual ao diâmetro de sua base, expresse [tex]V[/tex] em função de [tex]r[/tex].

Solução

---

(a) O volume do reservatório, [tex]V_R\,[/tex], é a soma do volume do cilindro circular reto, [tex]V_C[/tex], e o volume da semiesfera, [tex]V_S[/tex], que compõem o reservatório. Assim, vamos calcular separadamente [tex]V_C\,[/tex] e [tex]\,V_S[/tex].
Vamos aos cálculos.

• De acordo com o Lembrete (1), o volume do cilindro circular reto que compõe o reservatório é:

[tex]\qquad \qquad V_C=\pi\cdot r^2\cdot h\;\text{ unidades de volume}.[/tex]

• O volume da semiesfera de raio [tex]r[/tex] que compõe o reservatório é a metade do volume de uma esfera de raio [tex]r[/tex]. Logo, de acordo com o Lembrete (2), temos que:

[tex]\qquad \qquad V_S=\dfrac{\frac{4}{3} \cdot \pi \cdot r^3}{2}[/tex]
[tex]\qquad \qquad V_S=\dfrac{2}{3} \cdot \pi \cdot r^3\;\text{ unidades de volume}.[/tex]

Portanto, segue que:
[tex]\qquad V_R=V_C+V_S\\
\qquad V_R=\pi\cdot r^2\cdot h+\dfrac{2}{3} \cdot \pi \cdot r^3\\
\qquad \fcolorbox{black}{#eee0e5}{$V_R=\pi\, r^2 \left( h+\dfrac{2}{3}\, r \right)\;\text{ unidades de volume}$}\,.[/tex]

(b) Suponha, agora, que a altura do cilindro seja igual ao diâmetro de sua base. Assim, [tex]h=2r[/tex] e, portanto,
[tex] \qquad V_R=\pi\, r^2 \left( 2r+\dfrac{2}{3}\, r \right)[/tex]
[tex] \qquad V_R=\pi\, r^2 \left(\dfrac{8}{3}\, r \right)[/tex]
[tex] \qquad \fcolorbox{black}{#eee0e5}{$V_R=\dfrac{8}{3}\pi\, r^3\;\text{ unidades de volume}$}\,.[/tex]

---

Solução elaborada pelos Moderadores do Blog.