Problema
(Indicado a partir do 2º ano do E. M.)
(Adaptado do Portal da Matemática) Dispondo de sete cores distintas, de quantos modos podemos pintar as faces de um tronco de pirâmide cujas bases são pentágonos regulares de maneira que as bases tenham a mesma cor e todas as faces laterais tenham cores diferentes das bases e diferentes entre si?

Lembretes
► O número de permutações circulares dos elementos [tex]a_1,\, a_2,\,a_3,\,\dots\, ,\, a_n,\,[/tex] é dado por:
[tex]\qquad \qquad \left(PC\right)_n=(n-1) \cdot (n-2) \cdot\, \cdots \, 3 \cdot 2 \cdot 1 \, [/tex]
ou, utilizando fatorial,
[tex]\qquad \qquad \left(PC\right)_n=(n-1)![/tex].
► O número de Combinações simples de [tex]n[/tex] elementos, tomados [tex]r[/tex] a [tex]r[/tex], é dado por
[tex]\qquad \qquad C_{n\, ,\, r}=C_n^r=\dfrac{n!}{(n-r)!\, r!} \text{, com } n,r \in\mathbb{N} \text{ e }\, 0 \lt r\leqslant n[/tex].
► Princípio Fundamental da Contagem, ou Princípio Multiplicativo: Se
- uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
- uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma decisão Dk puder ser tomada de [tex]m_k [/tex] maneiras distintas e
- todas essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),
então o número total de maneiras de tomarmos sucessivamente essas [tex]k[/tex] decisões é igual ao produto
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k} \, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Solução
Na figura abaixo, temos um tronco de pirâmide, cujas bases são pentágonos regulares (faces superior e inferior) e as faces laterais são quadriláteros.
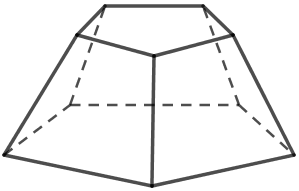
Antes de mais nada, note que sobrará uma cor; pois utilizaremos cinco cores para pintar as faces laterais e uma sexta cor para pintar as bases do tronco de pirâmide.
Faremos a escolha das cores em três etapas; observe a seguir.
- Temos [tex]\boxed{7} [/tex] possibilidades para escolher a cor das bases, sobrando [tex]6[/tex] cores para as faces laterais.
- Agora vamos escolher [tex]5[/tex] das [tex]6[/tex] cores que restaram para colorir as faces.
Isso pode ser feito de [tex]C_6^5=\dfrac{6!}{5!(6-5)!}=\boxed{6}[/tex] maneiras. - Escolhidas as [tex] 5[/tex] cores distintas, o total de maneiras de colorir as faces laterais é uma permutação circular de [tex]5[/tex].
Assim, as faces podem ser coloridas de [tex](5-1)!=4!=\boxed{24}[/tex] modos distintos.
Portanto, pelo Princípio Multiplicativo, podemos colorir as faces do tronco de pirâmide regular pentagonal de [tex]\,\fcolorbox{black}{#eee0e5}{$7\times 6 \times 24= 1008$}\, [/tex] modos diferentes.
Conforme alertamos no início desta solução, observe que sobrou uma cor e com ela poderíamos colorir uma das faces do tronco de pirâmide. Então [tex] 1008[/tex] é também o número de maneiras com que podemos pintar as faces desse tronco de uma pirâmide usando as [tex]7[/tex] cores iniciais.
Veja a seguir a solução independente desse novo problema.
Problema: De quantos modos podemos pintar as faces de um tronco de uma pirâmide, cujas bases são pentágonos regulares, usando [tex]7[/tex] cores diferentes e de maneira que todas as faces tenham cores distintas?
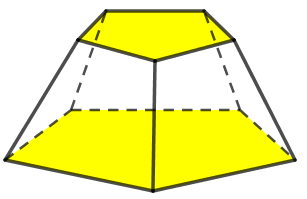
Solução: Na figura abaixo, temos um tronco de pirâmide, cujas bases são pentágonos regulares (faces superior e inferior, respectivamente) e as faces laterais são quadriláteros.

- Podemos escolher uma das [tex]7[/tex] cores para colorir a base superior, sobrando [tex]6[/tex] cores para colorir a base inferior.
Dessa forma, segue do Princípio Multiplicativo que há [tex]7 \cdot 6= \boxed{42}[/tex] formas de colorir as bases inferior e superior do tronco de pirâmide.
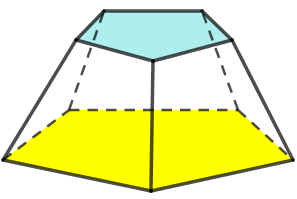
Sobram, então, cinco cores distintas para colorir as faces laterais.
- O total de maneiras para colorir as cinco faces é uma permutação circular de [tex]5[/tex], ou seja, [tex](5-1)!=4!=\boxed{24}[/tex].
Portanto, utilizando uma vez mais o Princípio Multiplicativo, podemos colorir as faces do tronco de pirâmide de [tex]\,\fcolorbox{black}{#eee0e5}{$42 \times 24= 1008$}\,[/tex] modos diferentes.
Solução elaborada pelos Moderadores do Blog.
