✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
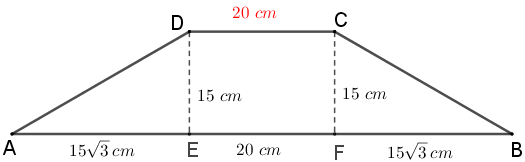
Calcule a medida aproximada, em centímetros quadrados, da área do trapézio isósceles [tex]ABCD[/tex] mostrado na figura.
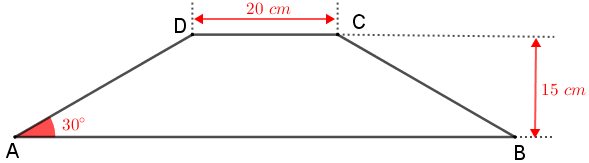
Lembretes:

✐ Para solucionar este problema, vamos precisar de uma das relações entre as medidas dos lados e dos ângulos internos de um triângulo retângulo. Vale a pena recordar essas relações!
Seja, então, um triângulo retângulo [tex]ABC[/tex], cujos lados têm comprimentos [tex]a,\, b,\, c\, [/tex] e os ângulos agudos têm medidas [tex]\alpha[/tex] e [tex]\beta[/tex], conforme indicado na figura.
Então:
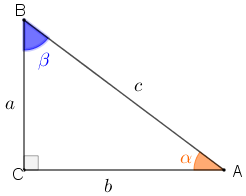
[tex]\bullet \, sen\, \hat{A}=sen\, \alpha=\dfrac{a}{c}=cos\, \beta=cos\, \hat{B}[/tex]
[tex]\bullet \, cos\, \hat{A}=cos\, \alpha=\dfrac{b}{c}=sen\, \beta=sen\, \hat{B}[/tex]
[tex]\bullet \, tan\, \hat{A}=tan\, \alpha=\dfrac{a}{b}[/tex]
[tex]\bullet \, tan\, \hat{B}=tan\, \beta=\dfrac{b}{a}[/tex]
✐ Congruência de triângulos retângulos:
Se dois triângulos retângulos têm ordenadamente congruentes um cateto e a hipotenusa, então estes triângulos são congruentes.
✐ Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY.[/tex]
Solução
A medida da área de um trapézio pode ser calculada utilizando-se a seguinte expressão:
[tex]\qquad \dfrac{\left(\text{base maior+base menor}\right)\times \text{altura}}{2}\,\,.[/tex]
Das três medidas que aparecem nessa fórmula, já temos o comprimento da chamada base menor, [tex]20\,\text{cm}[/tex], e comprimento da altura, [tex]15\,\text{cm}.[/tex]
Vamos, então, obter a medida que falta: o comprimento da base maior, ou seja, o comprimento de [tex]\overline{AB}.[/tex]
Para isso, sejam [tex]E[/tex] e [tex]F[/tex] pontos de [tex]\overline{AB}[/tex] tais que [tex]\overline{AB}[/tex] e [tex]\overline{DE}[/tex] sejam perpendiculares, assim como [tex]\overline{AB}[/tex] e [tex]\overline{CF}.[/tex] Então, [tex]DE=CF=15\,\text{cm}.[/tex]
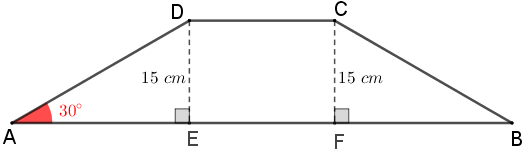
Como o trapézio é isósceles, então [tex]AD=BC[/tex]. Com isso, os triângulos retângulos [tex]AED[/tex] e [tex]BFC[/tex] são congruentes e, portanto a medida do ângulo [tex]C\hat{B}F\,[/tex] é [tex]\,30^\circ[/tex] e [tex]\,AE=FB.[/tex]
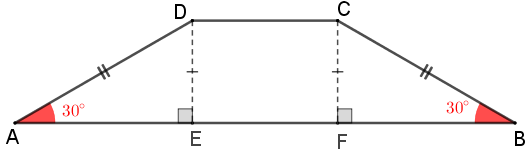
Utilizando a definição de tangente dada nos Lembretes, temos que [tex]tan\,30^\circ=\dfrac{DE}{AE}\,[/tex] e, consultando uma tabela trigonométrica, temos que [tex] tan\,30^\circ=\dfrac{\sqrt{3}}{3}[/tex]; logo, segue que:
[tex]\quad tan\,30^\circ=\dfrac{DE}{AE}\\
\quad \dfrac{\sqrt{3}}{3}=\dfrac{15}{AE}\\
\quad AE=\dfrac{15}{\frac{\sqrt{3}}{3}}\\
\quad AE=\dfrac{45}{\sqrt{3}}=\dfrac{45 \times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}=\dfrac{45 \times \sqrt{3}}{3}=15\,\sqrt{3}\,\,\text{cm}.\\[/tex]
Já podemos obter a medida da base maior do trapézio:
[tex]\quad AB=AE+EF+FB\\
\quad AB=15\,\sqrt{3}+20+15\,\sqrt{3}\\
\quad AB=30\,\sqrt{3}+20\,\,\text{cm}.\\[/tex]
Finalmente, a medida [tex]S[/tex] da área do trapézio é:
[tex]\qquad S= \dfrac{\left(\text{base maior+base menor}\right)\times \text{altura}}{2}\\
\qquad S= \dfrac{\left(\left(30\,\sqrt{3}+20\right)+20\right)\times 15}{2}\\
\qquad S= \left(15\,\sqrt{3}+20\right)\times 15\\
\qquad S=225\,\sqrt{3}+300\,\,\text{cm}^2[/tex]
ou seja, [tex]\fcolorbox{black}{#eee0e5}{$S\approx 689,71\,\text{cm}^2$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
