Problema
(Indicado a partir do 1º ano do E. M.)
Sejam [tex]x[/tex] e [tex]y[/tex] números reais tais que [tex]x^{2}+y^{2}=8x+6y-16[/tex]. Qual o maior valor possível de [tex]x[/tex]?

Lembrete
As raízes da equação do segundo grau [tex]~~ax^2+bx+c = 0~~[/tex] são dadas por
[tex]~~~~~~~~~~~~x_1 = \dfrac{-b+\sqrt{\Delta}}{2a}~~~[/tex] e [tex]~~~x_2 = \dfrac{-b-\sqrt{\Delta}}{2a}[/tex],
onde [tex]a,b,c[/tex] são números reais, com [tex]a\ne 0~[/tex], e [tex]~\Delta =b^2-4ac[/tex].
Solução 1
Podemos reescrever a igualdade fornecida no problema como
[tex] y^2-6y+\left(x^2-8x+16\right)=0~\qquad \textcolor{#800000}{(i)}[/tex]
e nessa forma, a igualdade pode ser vista como uma equação do segundo grau na incógnita [tex]y[/tex].
Como [tex]y[/tex] é um número real, a equação [tex]\textcolor{#800000}{(i)}[/tex] tem solução real e, portanto, seu discriminante é maior ou igual a zero ([tex]\Delta\geq 0[/tex]). Assim:
[tex]\qquad 6^2-4\cdot 1 \cdot (x^2-8x+16)\geq 0[/tex]
[tex]\qquad 36-4x^2+32x-64\geq 0[/tex]
[tex]\qquad x^2-8x+7\leq 0.\qquad \textcolor{#800000}{(ii)}[/tex]
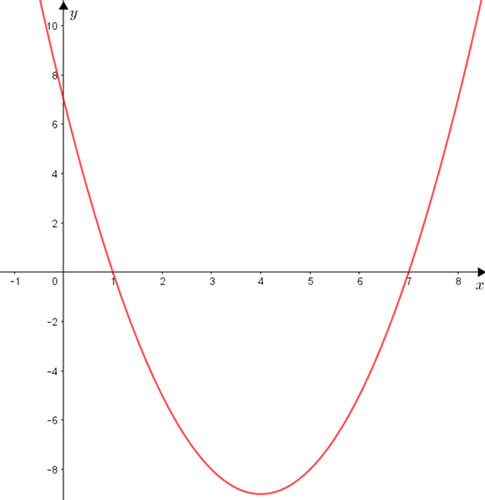
Podemos resolver a inequação do segundo grau [tex]\textcolor{#800000}{(ii)}[/tex] a partir do gráfico da função quadrática [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]f(x)=x^2-8x+7[/tex], que sabemos ser uma parábola, respondendo a seguinte pergunta:
Para que valores de [tex]x[/tex] temos [tex]f(x)\leq 0[/tex]?
E para responder essa pergunta, vamos encontrar os zeros da função [tex]f[/tex], ou de outra forma, as raízes da equação [tex]x^2-8x+7 = 0.[/tex] Utilizando o Lembrete, temos que as raízes da equação [tex]x^2-8x+7 = 0[/tex] são dadas por:
[tex] \qquad x_1 = \dfrac{8+\sqrt{36}}{2}=\dfrac{8+6}{2}=7 \qquad [/tex] e [tex]~~~\qquad x_2 = \dfrac{8-\sqrt{36}}{2}=\dfrac{8-6}{2}=1[/tex].
Dessa forma, a variação de sinal da função [tex]f[/tex] poder ser assim esquematizada:
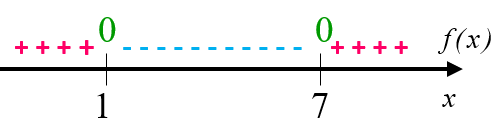
Concluímos, então, que [tex]f(x)\leq 0[/tex] para valores de [tex]x[/tex] tais que [tex] 1\leq x\leq 7[/tex] e, assim, o maior valor que [tex]x[/tex] pode assumir é [tex] ~\fcolorbox{black}{#eee0e5}{$x=7$}~.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Podemos reescrever a igualdade fornecida no problema como
[tex] y^2-6y+\left(x^2-8x+16\right)=0~\qquad \textcolor{#800000}{(i)}[/tex]
e, então, a igualdade pode ser vista como uma equação do segundo grau na incógnita [tex]y[/tex].
Como [tex]y[/tex] é um número real, a equação [tex]\textcolor{#800000}{(i)}[/tex] tem solução real e, portanto, seu discriminante é maior ou igual a zero ([tex]\Delta\geq 0[/tex]). Assim:
[tex]\qquad 6^2-4\cdot 1 \cdot (x^2-8x+16)\geq 0[/tex]
[tex]\qquad 36-4x^2+32x-64\geq 0[/tex]
[tex]\qquad x^2-8x+7\leq 0.\qquad \textcolor{#800000}{(ii)}[/tex]
Trabalhando algebricamente a desigualdade [tex]\textcolor{#800000}{(ii)}[/tex], segue a seguinte sequência de desigualdades equivalentes:
[tex]\qquad \begin{align*} x^2-8x+7\leq 0 &\iff (x-4)^2-9\leq 0\\
&\iff (x-4)^2\leq 9 \\
&\iff \sqrt{(x-4)^2}\leq \sqrt{9} \\
&\iff |x-4|\leq 3 \\
&\iff -3\leq x-4\leq 3 \\
&\iff 1\leq x\leq 7 . \end{align*}[/tex]
Dessa forma, [tex]\boxed{x^2-8x+7\leq 0 \iff 1\leq x\leq 7}[/tex] e o maior valor que [tex]x[/tex] pode assumir é [tex] ~\fcolorbox{black}{#eee0e5}{$x=7$}~.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 3
Podemos reescrever a equação dada no problema fazendo dois completamentos de quadrado (Se você não se lembra desse procedimento, dê uma passadinha nesta Sala de Leitura.). Observe:
[tex]\qquad x^2-8x+y^2-6y+16=0[/tex]
[tex]\qquad \left(x^2-8x \right)+\left(y^2-6y\right)=-16[/tex]
[tex]\qquad \left(x^2-8x \right)+16+\left(y^2-6y\right)+9=-16+16+9[/tex]
[tex]\qquad \left(x^2-8x +16\right)+\left(y^2-6y+9 \right)=9[/tex]
[tex]\qquad (x-4)^2+(y-3)^2=9.\qquad \textcolor{#800000}{(iii)}[/tex]
Em um plano cartesiano [tex]xOy[/tex], a equação [tex]\textcolor{#800000}{(iii)}[/tex] representa uma circunferência de centro no ponto [tex]C=(4,3)[/tex] e raio [tex]3[/tex].
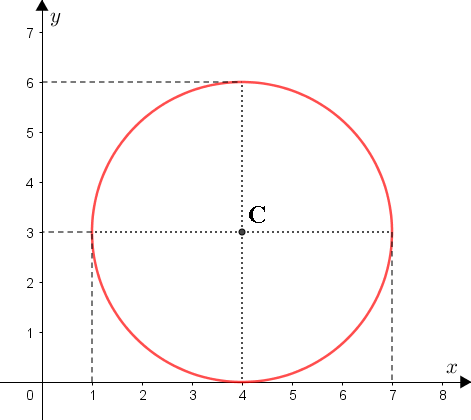
Portanto o maior valor que [tex]x[/tex] pode assumir é [tex] ~\fcolorbox{black}{#eee0e5}{$x=7$}~.[/tex]
Solução elaborada pelos Moderadores do Blog.
