✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
(XXXV Olimpiada Matemática Española – Adaptado) Uma empresa produz semanalmente 300 unidades de um determinado produto, quantidade essa que é vendida totalmente ao preço de 600 reais cada unidade.
Ao longo de um período de tempo observou-se que, se o preço das unidades variava, as vendas também variavam de acordo com a seguinte relação:
- a cada 7 reais de aumento ou de desconto no preço de cada unidade, a venda diminuía ou aumentava em 3 unidades, respectivamente.
A partir dessas observações, a que preço a receita seria máxima?

Lembretes
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,\, a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
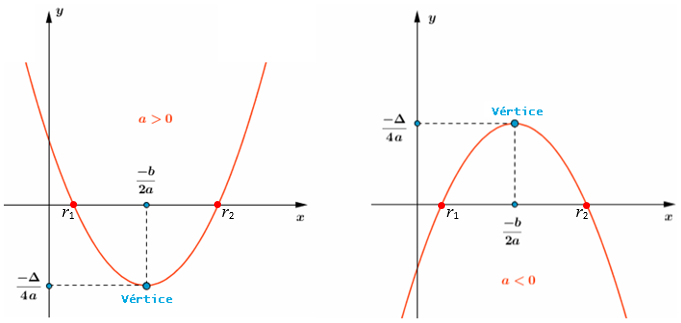
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola do gráfico de [tex]h[/tex] são dadas por:
[tex]\qquad \qquad (x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex],
sendo que [tex]x_v=\dfrac{-b}{2a}\, [/tex] e [tex]\, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Particularmente, se [tex]\Delta \gt 0[/tex], [tex]x_v[/tex] é a média entre as duas raízes de [tex]h[/tex]: [tex]x_v=\dfrac{r_1+r_2}{2}\, .[/tex]
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução
Seja [tex]x[/tex] uma possível variação em reais do preço do produto em questão. (Perceba que [tex]x[/tex] pode ser um número real positivo, negativo ou zero, conforme o preço inicial aumente, diminua ou permaneça o mesmo, respectivamente.)
Então,
- o novo preço da unidade do produto será [tex]\boxed{600 + x}[/tex] reais.[tex]\qquad \textcolor{#800000}{(i)}[/tex]
De acordo com a regra de variação dada no problema,
- a quantidade de produtos vendidos com o novo preço será [tex]\boxed{300\textcolor{red}{-}\dfrac{3}{7}x}.\qquad \textcolor{#800000}{(ii)}[/tex]
(Não estranhe o negativo que apareceu nessa última expressão. Lembre-se de que quando o preço aumenta, as vendas diminuem; e quando o preço diminui, as vendas aumentam.)
Assim, por [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], a receita resultante da venda do produto a um preço unitário de [tex](600 + x)[/tex] reais será
[tex]\boxed{(600 + x)\times \left(300-\dfrac{3}{7}x\right)}.[/tex]
Para resolver o problema, precisamos calcular um valor para [tex]x[/tex] que acarretará a receita máxima. Para isso, observe que a receita é função da variação [tex]x[/tex], em reais, do preço do produto. Logo, podemos explicitar essa relação da receita com a variação de preço [tex]x[/tex] definindo a seguinte função:
[tex]f: \mathbb{R} \rightarrow \mathbb{R} \\
\quad f(x)=(600 + x)\times \left(300-\dfrac{3}{7}x\right).[/tex]
Desenvolvendo a expressão que define [tex]f(x)[/tex] obtemos:
[tex]\qquad f(x)=(600 + x)\times \left(300-\dfrac{3}{7}x\right)\\
\qquad f(x)=180000-\dfrac{1800}{7}x+300x-\dfrac{3}{7}x^2\\
\qquad f(x)=-\dfrac{3}{7}x^2+\dfrac{300}{7}x+180000,[/tex]
e assim temos que
[tex]f: \mathbb{R} \rightarrow \mathbb{R} \\
\quad f(x)=-\dfrac{3}{7}x^2+\dfrac{300}{7}x+180000.[/tex]
Note que [tex]f[/tex] é uma função quadrática cujo gráfico é uma parábola com concavidade voltada para baixo. Com isso, se as coordenadas do vértice dessa parábola forem [tex]\left(x_v,y_v\right)[/tex], então [tex]y_v[/tex] será a receita máxima e [tex]x_v[/tex] será a variação do preço de venda que produz a receita máxima. Vamos, portanto, calcular [tex]x_v[/tex]:
[tex]\qquad x_v=\dfrac{-b}{2a}\\
\qquad x_v=\dfrac{-\frac{300}{7}}{2\cdot \left(-\frac{3}{7}\right)}\\
\qquad x_v=\dfrac{100}{2}\\
\qquad \boxed{x_v=50}.[/tex]
Poderíamos até calcular a receita máxima calculando [tex]y_v[/tex], ou mesmo a imagem [tex]f(x_v)[/tex], mas não é isso que o problema está pedindo. O que precisamos calcular é o preço unitário de venda do produto que provocaria essa receita máxima e para isso basta substituir [tex]x=50[/tex] na igualdade [tex]\textcolor{#800000}{(i)}[/tex]: [tex]600 + x_v=600+50=650.[/tex]
Portanto, dentro dos parâmetros do problema, o preço individual do produto que resulta na receita máxima é [tex]\, \fcolorbox{black}{#eee0e5}{$R\$\, 650,00$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |