✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
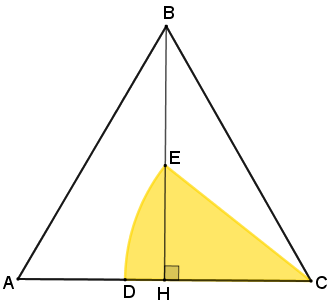
(ONEM 2010) Na figura, o segmento [tex]\overline{BH}[/tex] é uma altura do triângulo equilátero [tex]ABC[/tex], cujos lados têm comprimentos [tex]6\sqrt{3}\,cm[/tex], e [tex]D[/tex] é um ponto do segmento [tex]\overline{AC}[/tex] tal que a distância entre os pontos [tex]D[/tex] e [tex]H[/tex] é [tex]3\left(2-\sqrt{3}\right)\, cm.[/tex]
Sabendo que [tex]E[/tex] é um ponto do segmento [tex]\overline{BH}[/tex], determine a medida da área do setor circular [tex]ECD.[/tex]
Ajuda
✐ Definição: Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a,\, b,\, h[/tex], respectivamente. Seja [tex]\theta[/tex] a medida em graus de um dos ângulos agudos desse triângulo, [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].
Chamamos cosseno de [tex]\theta[/tex], e denotamos por [tex]cos\, \theta[/tex], a razão entre os comprimentos do cateto adjacente a [tex]\theta[/tex] e da hipotenusa: [tex]\boxed{ cos\, \theta= \dfrac{b}{h}}.[/tex]
✐ No estudo da trigonometria, alguns ângulos são bastante utilizados e devido à frequência com que eles surgem em problemas e à importância que eles têm para a Geometria são denominados ângulos especiais ou ângulos fundamentais. São eles os ângulos com medidas iguais a: [tex]30^\circ[/tex], [tex] 45^{\circ} [/tex] e [tex]60^\circ[/tex].
Os senos, cossenos e tangentes desses ângulos são:
a) [tex]\, \, sen\, 30^{\circ}=\dfrac{1}{2}\qquad\qquad\, \, \, \, cos\, 30^{\circ}=\dfrac{\sqrt{3}}{2}\qquad\qquad tg\, 30^{\circ}=\dfrac{\sqrt{3}}{3}[/tex] .
b) [tex]\, \, sen\, 45^{\circ}=\dfrac{\sqrt{2}}{2}\qquad\qquad[/tex] [tex] cos\, 45^{\circ}=\dfrac{\sqrt{2}}{2}\qquad\qquad[/tex] [tex] tg\, 45^{\circ}=1[/tex] .
c) [tex]\, \, sen\, 60^{\circ}=\dfrac{\sqrt{3}}{2}\qquad\qquad[/tex] [tex] cos\, 60^{\circ}=\dfrac{1}{2}\qquad\qquad[/tex] [tex]\, \, \, \, tg\, 60^{\circ}=\sqrt{3}[/tex] .
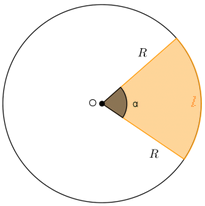
✐ Área de um setor circular de raio [tex]R[/tex] e [tex]\alpha[/tex] graus:
[tex]\qquad \qquad \boxed{A_{setor}=\dfrac{\pi\cdot R^{\, 2} \cdot \alpha}{360}}[/tex].
✐ Uma altura de um triângulo equilátero é também mediana e bissetriz.
✐ Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução
Este problema é um desafio não pelo raciocínio que ele exige, mas pela quantidade de informações que ele utiliza! Vamos à solução.
Como o segmento [tex]\overline{BH}[/tex] é uma altura do triângulo equilátero [tex]ABC[/tex], então [tex]\overline{BH}[/tex] é também uma mediana. Assim:
[tex]\qquad HC=\dfrac{AC}{2}=\dfrac{6\sqrt{3}}{2}=3\sqrt{3}\, cm[/tex]
e, consequentemente, o comprimento [tex]r[/tex], em centímetros, do raio do setor circular [tex]ECD[/tex] é dado por:
[tex]\qquad r=DC=EC=DH+HC\\
\qquad r=3\left(2-\sqrt{3}\right)+3\sqrt{3}\\
\qquad r=6-\cancel{3\sqrt{3}}+\cancel{3\sqrt{3}}\\
\qquad r=6\, cm.[/tex]
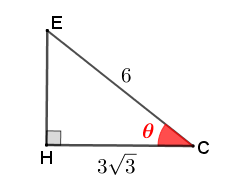
Observemos agora o triângulo retângulo [tex]EHC.[/tex]
Consultando as informações da AJUDA, vemos que se [tex]\textcolor{red}{\theta}[/tex] é a medida do ângulo central do setor circular, então:
[tex]\qquad cos\, \textcolor{red}{\theta}=\dfrac{HC}{EC}=\dfrac{3\sqrt{3}}{6}=\dfrac{\sqrt{3}}{2}\\[/tex]
e, portanto, [tex]\textcolor{red}{\theta=30^\circ}.[/tex]
Já temos a medida em graus do setor circular [tex]ECD[/tex], assim como o seu raio. Logo, utilizando a fórmula da área de um setor circular apresentada na AJUDA, temos que:
[tex] A_{setor}=\dfrac{\pi\cdot 6^2 \cdot 30}{360}=3\pi[/tex]
e com isso podemos concluir que a medida da área do setor circular [tex]ECD[/tex] é [tex]\, \fcolorbox{black}{#ffdc22}{$3\pi\, cm^2$}\, [/tex], aproximadamente [tex]\, \fcolorbox{black}{#ffdc22}{$9,42\, cm^2$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |