Problema
(Indicado a partir do 8º ano do E. F.)
(Adaptado do livro Círculos Matemáticos) As amigas Adriana e Suellen estavam estudando para uma prova de matemática, cujo conteúdo abordado seria paridade. A segunda questão da lista de exercícios que elas estavam resolvendo era a seguinte:
- A equação [tex] \, \boxed{ \dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{d}=1} \, [/tex] possui solução no conjunto dos números ímpares?
Suellen chegou à conclusão de que sim e Adriana de que não.
Qual delas acertou a questão?

Ajuda
Em várias situações é possível determinarmos a paridade de expressões envolvendo números naturais, a partir da paridade desses números, sem sequer calcular as expressões.
Particularmente, as tabelinhas abaixo ilustram situações de paridade que irão aparecer na solução deste problema:
- A soma de dois números naturais de mesma paridade é par.
- A soma de dois números naturais de paridade oposta é ímpar.
- O produto de dois números naturais só será ímpar se os dois números forem ímpares.
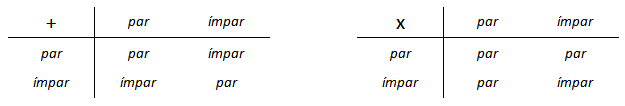
(Se precisar, visite esta Sala.)
Solução
Observe a sequência de implicações abaixo:
\begin{equation}
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}=1\Rightarrow \frac{bcd+acd+abd+abc}{abcd}=1 \Rightarrow\\
\Rightarrow bcd+acd+abd+abc=abcd.\end{equation}
Assim, números que satisfaçam a igualdade
[tex]\qquad \qquad \boxed{ \dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{d}=1} \, [/tex],
também satisfazem a igualdade
[tex]\qquad \qquad \, \boxed{ bcd+acd+abd+abc=abcd} \, .\;\;\;\;\;\;\;\;\;\; \textcolor{#800000}{(1)}[/tex]
Suponha que os números [tex]a,b, c[/tex] e [tex]d[/tex] são números ímpares.
Notemos que cada uma das parcelas [tex]bcd,\;acd,\;abd[/tex] e [tex]abc[/tex] é um número ímpar, já que o produto de três números ímpares resulta em um número ímpar.
- Assim, a soma [tex]bcd+acd+abd+abc[/tex] resulta em um número par.
- Agora, como [tex]a,b, c[/tex] e [tex]d[/tex] são números ímpares teremos que o produto [tex]abcd[/tex] será um número ímpar.
Com isso, da equação [tex]\textcolor{#800000}{(1)}[/tex], teremos que um número ímpar é também um número par. E isso é impossível!

Portanto, a equação [tex] \, \boxed{ \dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{d}=1} \, [/tex] NÃO possui solução no conjunto dos números ímpares, ou seja, Adriana estava correta em sua resposta.
 |
Para obter outros problemas envolvendo paridade, visite nesta Sala.
|
Solução elaborada pelos Moderadores do Blog.
