✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
(Extraído da XV Olimpíada Regional de Matemática de Santa Catarina – 2012) A partir de cinco quadrados de lados com comprimentos de [tex]1 \, cm[/tex] foi construído o polígono na forma de cruz mostrado na Figura 1.
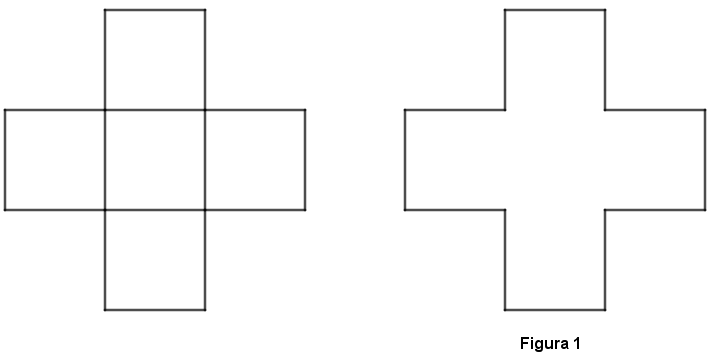
Esse polígono foi rotacionado em torno de seu centro, segundo um ângulo de [tex]45^\circ[/tex], resultando na Figura 2.
Parte dessa figura foi colorida de vermelho e destacada como na Figura 3.
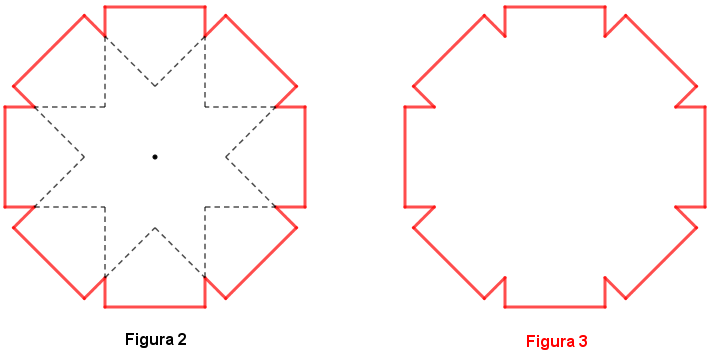
Calcule o comprimento do perímetro da Figura 3.
Solução
Devido à simetria da construção, o comprimento [tex]\textcolor{red}{C}[/tex] do perímetro a ser calculado equivale a oito vezes o comprimento [tex]\textcolor{#3BB9FF}{P}[/tex] do perímetro colorido de azul na figura em questão.
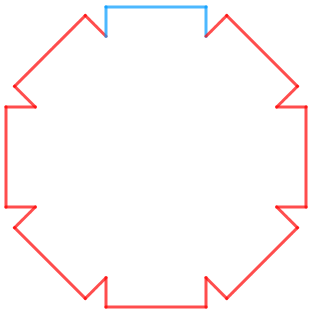
Para calcular esse comprimento, vamos desenhar e ampliar parte da Figura 2.
Observe que dos três segmentos de reta azuis já conhecemos o comprimento do maior; precisamos então do comprimento dos dois menores, comprimento esse que denotaremos por [tex]y[/tex].
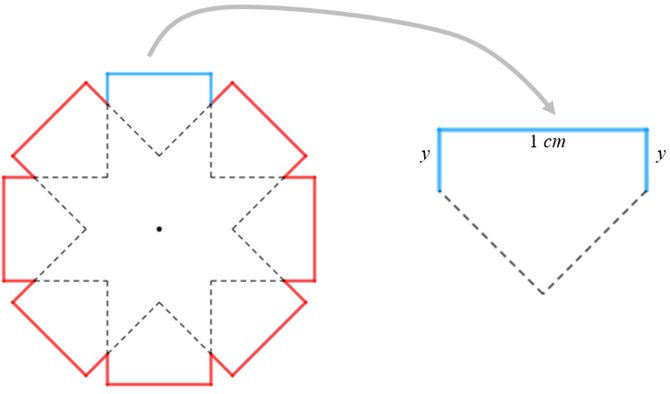
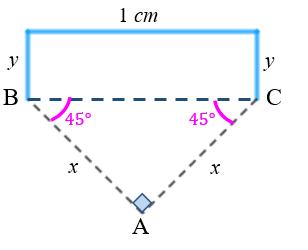
Como o ponto [tex]A[/tex] destacado na figura ao lado é vértice de um quadrado (Veja figura inicial do problema), o triângulo [tex]ABC[/tex] é retângulo. Além disso, devido à rotação de [tex]45^\circ[/tex], as medidas dos ângulos de vértices em [tex]B[/tex] e [tex]C[/tex] são ambas [tex]45^\circ[/tex] e, portanto, o triângulo [tex]ABC[/tex] é isósceles.
Denotando a medida em centímetros dos segmentos [tex]AB[/tex] e [tex]AC[/tex] por [tex]x[/tex], do Teorema de Pitágoras, segue que:
[tex]\qquad x^2+x^2=1^2[/tex]
[tex]\qquad 2x^2=1[/tex]
[tex]\qquad x^2=\dfrac{1}{2}[/tex]
[tex]\qquad x =\sqrt{\dfrac{1}{2}}[/tex], já que [tex]x \gt 0[/tex]
[tex]\qquad \boxed{x =\dfrac{\sqrt{2}}{2} \, cm}.[/tex]
Para calcular o comprimento do perímetro colorido de azul, basta determinar [tex]y[/tex] e, para isso, observemos uma vez mais parte da Figura 2.
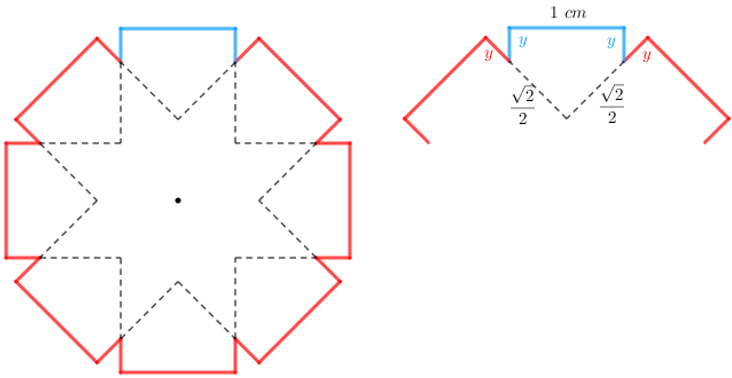
Perceba que [tex]y+\dfrac{\sqrt{2}}{2}[/tex] é o comprimento do lado de um dos cinco quadrados que originaram a figura final; logo, segue que:
[tex]\qquad y+\dfrac{\sqrt{2}}{2}=1[/tex]
[tex]\qquad y=1-\dfrac{\sqrt{2}}{2}[/tex]
e, portanto, o comprimento [tex]\textcolor{#3BB9FF}{P}[/tex] do perímetro colorido de azul é:
[tex]\qquad \textcolor{#3BB9FF}{P}=2y+1[/tex]
[tex]\qquad \textcolor{#3BB9FF}{P}=2\cdot \left(1-\dfrac{\sqrt{2}}{2}\right)+1[/tex]
[tex]\qquad \textcolor{#3BB9FF}{P}=2-\sqrt{2}+1[/tex]
[tex]\qquad \textcolor{#3BB9FF}{P=3-\sqrt{2} \, cm}.[/tex]
Finalmente, como [tex]\textcolor{red}{C}=8\textcolor{#3BB9FF}{P}[/tex], então:
[tex]\qquad \textcolor{red}{C}=8\textcolor{#3BB9FF}{P}[/tex]
[tex]\qquad \textcolor{red}{C}=8 \cdot \textcolor{#3BB9FF}{\left(3-\sqrt{2}\right)}[/tex]
[tex]\qquad \textcolor{red}{C=24-8\sqrt{2} \, cm}[/tex].
Assim, o comprimento do perímetro da Figura 3 é [tex] \, \fcolorbox{black}{#ffd3d3}{$24-8\sqrt{2} \, cm$} \, [/tex], aproximadamente, [tex] \, \fcolorbox{black}{#ffd3d3}{$12,7 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
