.Problemão: Caminhos distintos

Problema
(Indicado a partir do 2º ano do E. M.)

(IME– Adaptado) Em um jogo, quatro cidades, [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex], são conectadas por estradas conforme mostra a figura abaixo.

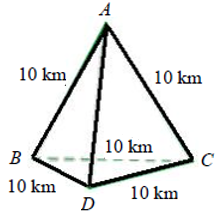
Quantos percursos diferentes começam e terminam na cidade [tex]A[/tex], e possuem exatamente [tex]50\;km[/tex]?

Ajuda

✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo: Se

uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas,
[tex]\cdots[/tex]
uma decisão Dk puder ser tomada de [tex]m_k [/tex] maneiras distintas,
e todas essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),

então o número total de maneiras de tomarmos sucessivamente essas [tex]k[/tex] decisões é igual ao produto
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k}\, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)

Solução

Como devemos percorrer [tex]50\;km[/tex], necessariamente passaremos por [tex]6[/tex] cidades. Obviamente, a primeira e a última cidades devem ser a [tex]A[/tex].
Vamos dividir o problema em duas partes:
1º) Caminhos que não passam pela cidade [tex]A[/tex].
Devemos escolher [tex]6[/tex] cidades para completar os [tex]50\;km[/tex].

Para a primeira cidade só há uma possibilidade ([tex]A[/tex]);
Para a segunda cidade há três possibilidades ([tex]B[/tex], [tex]C[/tex] ou [tex]D[/tex]);
Para a terceira cidade há duas possibilidades (não pode ser a [tex]A[/tex] nem a cidade na qual se estava anteriormente);
Para a quarta cidade há duas possibilidades (não pode ser a [tex]A[/tex] nem a cidade na qual se estava anteriormente);
Para a quinta cidade há duas possibilidades (não pode ser a [tex]A[/tex] nem a cidade na qual se estava anteriormente) e
Para a sexta cidade só há uma possibilidade ([tex]A[/tex]).

Assim, pelo Princípio Multiplicativo, existem
[tex]\qquad \qquad 1 \times 3 \times 2 \times 2 \times 2 \times 1 = \boxed{24 \; caminhos}.[/tex]

2º) Caminhos que passam pela cidade [tex]A[/tex].
Note que a passagem pela cidade [tex]A[/tex], antes de terminar os [tex]50\;km[/tex], só pode ocorrer uma vez e deve ser na terceira ou na quarta cidades. Vamos contar separadamente esses dois casos.

Passando por [tex]A[/tex] na terceira cidade:

Para a primeira cidade só há uma possibilidade ([tex]A[/tex]);
Para a segunda cidade há três possibilidades ([tex]B[/tex], [tex]C[/tex] ou [tex]D[/tex]);
Para a terceira cidade há uma possibilidade ([tex]A[/tex]);
Para a quarta cidade há três possibilidades ([tex]B[/tex], [tex]C[/tex] ou [tex]D[/tex]);
Para a quinta cidade há duas possibilidades (não pode ser a [tex]A[/tex] nem a cidade na qual se estava anteriormente) e
Para a sexta cidade só há uma possibilidade ([tex]A[/tex]).

Pelo Princípio Multiplicativo:
[tex]\qquad \qquad 1 \times 3 \times 1 \times 3 \times 2 \times 1 = \boxed{18 \; caminhos}.[/tex]

Passando por [tex]A[/tex] na quarta cidade:

Para a primeira cidade só há uma possibilidade ([tex]A[/tex]);
Para a segunda cidade há três possibilidades ([tex]B[/tex], [tex]C[/tex] ou [tex]D[/tex]);
Para a terceira cidade há duas possibilidades (não pode ser a [tex]A[/tex] nem a cidade na qual se estava anteriormente);
Para a quarta cidade há uma possibilidade ([tex]A[/tex]);
Para a quinta cidade há três possibilidades ([tex]B[/tex], [tex]C[/tex] ou [tex]D[/tex]) e
Para a sexta cidade só há uma possibilidade ([tex]A[/tex]).

Pelo Princípio Multiplicativo:
[tex]\qquad \qquad 1 \times 3 \times 2 \times 1 \times 3 \times 1 = \boxed{18 \; caminhos}.[/tex]

Logo, temos no total [tex]\fcolorbox{black}{#eee0e5}{$24+18+18=60$}[/tex] caminhos que satisfazem as condições do problema.

Solução elaborada pelos Moderadores do Blog.