Algumas aplicações de recorrências
|
|
Nesta Sala, vamos discutir três interessantes exemplos de problemas de Matemática modelados e resolvidos utilizando-se recorrências. |
Exemplo 1
Em uma bancada, há dez lâmpadas enfileiradas e cada uma delas pode estar acesa ou apagada.

► Quantas são as configurações possíveis para essas lâmpadas, de modo que não haja lâmpadas adjacentes acesas?
Exemplo 2
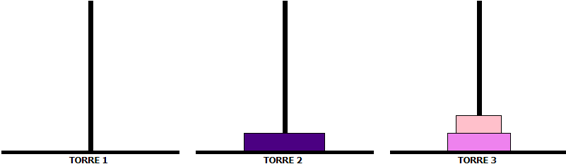
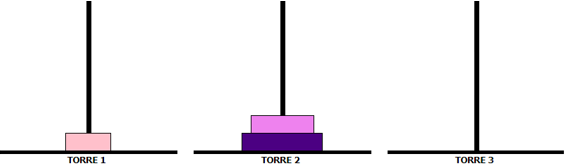
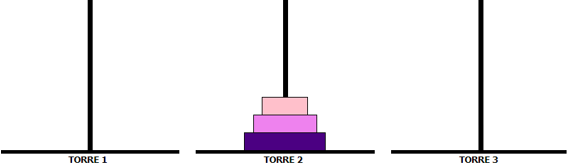
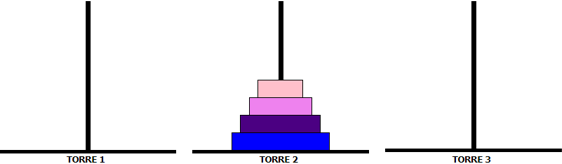
A Torre de Hanói é um dos mais famosos jogos de Matemática. Ele consiste de uma base contendo três pilares (hastes), em um dos quais está disposta uma torre formada por alguns discos colocados uns sobre os outros, em ordem crescente de diâmetro, de cima para baixo. O número de discos pode variar. Observe a disposição inicial de um jogo com seis discos.
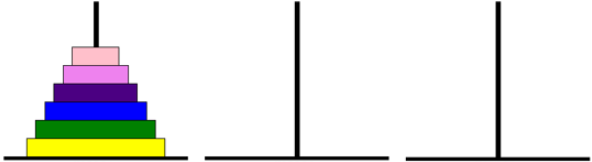
Esse jogo tem como objetivo deslocar todos os discos de um pilar para outro qualquer, obedecendo a duas regras:
(1) Mover apenas um disco por vez.
(2) Um disco com diâmetro maior nunca pode ficar sobre um disco com diâmetro menor.
► Qual o número mínimo de movimentos necessários para resolver o jogo da Torre de Hanói com seis discos?
 O inventor do jogo Torre de Hanói foi o matemático francês Édouard Lucas (1842-1891). O próprio criador do jogo elaborou a seguinte lenda:
O inventor do jogo Torre de Hanói foi o matemático francês Édouard Lucas (1842-1891). O próprio criador do jogo elaborou a seguinte lenda:
“No começo dos tempos, Deus criou a Torre de Brahma, que contém três hastes de diamante, e colocou na primeira haste 64 discos de ouro maciço. Deus chamou seus sacerdotes e ordenou-lhes que transferissem todos os discos para a terceira haste, seguindo as regras acima descritas. Os sacerdotes, então, obedeceram e começaram o trabalho de remoção dos discos, dia e noite.
Segundo Deus, quando eles terminarem o trabalho, a Torre de Brahma irá ruir e o mundo acabará…”
Com o applet abaixo, você poderá jogar a Torre de Hanói
com até treze discos. Que tal tentar?
Applet – Torre de Hanói
Para utilizar o applet:
[tex] \qquad \textcolor{#589386}{\bullet}[/tex] Espere o aplicativo carregar.
[tex] \qquad \textcolor{#589386}{\bullet}[/tex] Selecione a quantidade de discos.
[tex] \qquad \textcolor{#589386}{\bullet}[/tex] Observe a quantidade mínima de movimentos fornecida pelo aplicativo.
[tex] \qquad \textcolor{#589386}{\bullet}[/tex] Para mover um disco, clique sobre ele e, em seguida, clique na haste para a qual ele será movido.
[tex] \qquad \textcolor{#589386}{\bullet}[/tex] Se precisar reiniciar o jogo, clique no botão [tex]\boxed {\text{Reset}}[/tex], no canto superior esquerdo do aplicativo.
OBMEP_srg, criado com o GeoGebra
Adaptado de: Patrícia Coelho Barbosa
Exemplo 3
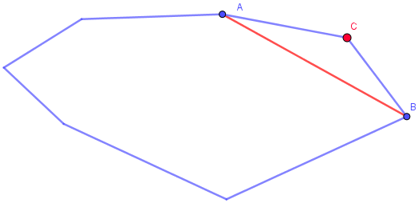
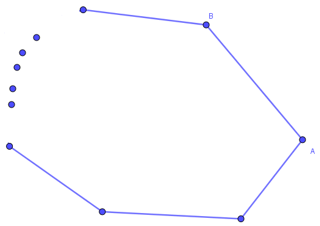
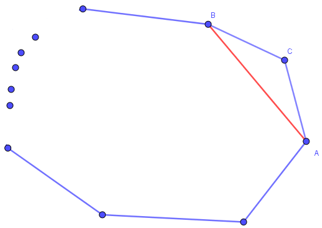
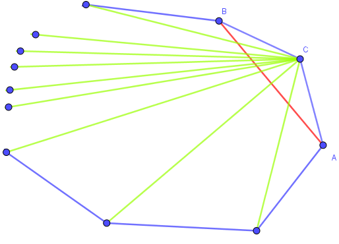
► Sabendo que um polígono convexo de [tex]24[/tex] lados possui [tex]x[/tex] diagonais, determine, em função de [tex]x[/tex], o número de diagonais do polígono convexo de [tex]25[/tex] lados.
Comentários Finais
Observem que, tanto no jogo da Torre de Hanói quanto no problema das diagonais, encontramos uma relação que expressa o termo [tex]n[/tex] das respectivas sequências em função apenas do termo [tex]n-1[/tex]:
[tex]\qquad \qquad a_{n}=2a_{n-1}+1 \qquad \qquad [/tex] [tex]\qquad \qquad d_{n+1}=d_{n}+n-1 \, .[/tex]
Por isso, essas relações são ditas Recorrências de Primeira Ordem. Já no problema das lâmpadas, encontramos uma relação que expressa o termo [tex]a_{n}[/tex] em função de [tex]a_{n-1}[/tex] e [tex]a_{n-2}[/tex]; esse tipo de relação recebe o nome de Recorrência de Segunda Ordem.
As discussões gerais sobre as classificações das fórmulas de recorrência e sobre a obtenção de fórmulas fechadas para recorrências não serão feitas nesta Sala de Estudo, pois fogem ao nosso objetivo neste momento, que é apresentar o raciocínio recursivo.
Equipe COM – OBMEP