Problema
(Indicado a partir do 1º ano do E. M.)
Considere um triângulo arbitrário [tex]ABC[/tex]. Sobre o lado [tex]\overline{AC}[/tex] tome um ponto [tex]P[/tex] e trace paralelas aos lados [tex]\overline{AB}[/tex] e [tex]\overline{BC}[/tex], encontrando os lados [tex]\overline{AB}[/tex] e [tex]\overline{BC}[/tex] nos pontos [tex]M[/tex] e [tex]N[/tex], respectivamente, como na figura.
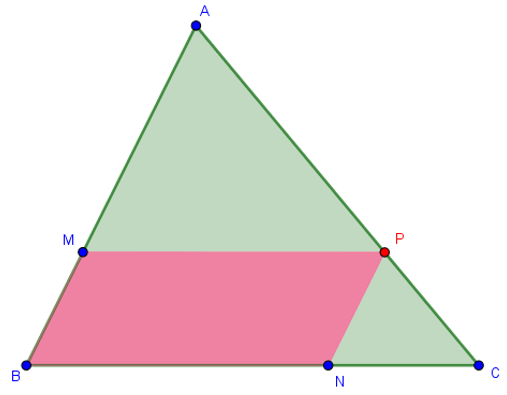
Determine a posição do ponto [tex]P[/tex] de maneira que o paralelogramo [tex]BNPM[/tex] possua área máxima.

Lembretes e notação
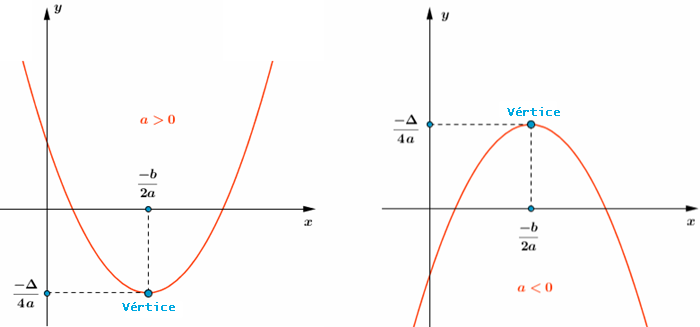
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c, \, a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a} \, [/tex] e [tex] \, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
[tex]{\color{#800000}(3)}[/tex] Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex] , por [tex]\overline{XY}[/tex] , e o seu comprimento por [tex]XY[/tex].
Solução 1
Observe a figura do problema. Como [tex]BNPM[/tex] é um paralelogramo, então os triângulos [tex]ABC[/tex] e [tex]PNC[/tex] são semelhantes, uma vez que seus lados são paralelos e, consequentemente, seus ângulos internos são congruentes. Notemos que a razão de semelhança desses triângulos é [tex] \boxed{k=\frac{PC}{AC}} \, .[/tex]
Sabemos que a área [tex]A_p[/tex] de um paralelogramo é [tex]A_p=(medida\; da\;base)\times (medida\;da\;altura)[/tex]; assim, a área do paralelogramo [tex]BNPM[/tex] é dada por
\begin{equation}A_p=BN\times (altura\;do\;\Delta (PNC)).\;\;\;\;\;\;\; \textcolor{#800000}{(i)}\end{equation}
Mas, pela semelhança dos triângulos [tex]ABC[/tex] e [tex]PNC[/tex] temos que
\begin{equation}altura\;do\;\Delta (PNC)=k\times altura\;do\;\Delta (ABC).\;\;\;\;\;\; \textcolor{#800000}{(ii)}\end{equation}
Então, por [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex]:
\begin{equation}A_p=BN\times k\times (altura\;do\;\Delta (ABC)).\;\;\;\;\;\; \textcolor{#800000}{(iii)}\end{equation}
Notemos que
\begin{equation}BN=BC-NC=BC-k\times BC=(1-k)\times BC, \;\;\;\;\;\; \textcolor{#800000}{(iv)}
\end{equation}
Assim, substituindo [tex]\textcolor{#800000}{(iv)}[/tex] em [tex]\textcolor{#800000}{(iii)}[/tex], obtemos que
\begin{equation}
A_p=[(1-k) \times BC] \times k\times (altura\;do\;\Delta (ABC))
\end{equation}
ou, ainda,
\begin{equation}
A_p=(1-k) \times k\times \left[(altura\;do\;\Delta (ABC)) \times BC\right]. \;\;\;\;\;\;\; \textcolor{#800000}{(v)}
\end{equation}
Observe agora que o produto [tex](altura\;do\;\Delta (ABC)) \times BC[/tex] é uma constante positiva, pois é um produto de medidas do triângulo [tex]ABC[/tex], que é fixo, embora tenha sido escolhido arbitrariamente.
Assim, se [tex]z=(altura\;do\;\Delta (ABC)) \times BC[/tex], então [tex]z\gt 0[/tex] e, por [tex]\textcolor{#800000}{(v)}[/tex], segue que:
\begin{equation}
A_p=-zk^2+zk.\;\;\;\;\;\; \textcolor{#800000}{(vi)}
\end{equation}
A igualdade [tex]\textcolor{#800000}{(vi)}[/tex] mostra que a área do paralelogramo é dada por uma função do segundo grau na variável [tex]k[/tex], com coeficiente líder [tex]-z\lt 0[/tex]. Logo, o valor máximo da área, de acordo com o Lembrete, ocorrerá quando
\begin{equation}
\boxed{k=-\frac{z}{-2z} =\frac{1}{2}} \, .\end{equation}
Neste caso, comparando as duas expressões para [tex]k[/tex], segue que:
[tex]\qquad \dfrac{1}{2}=k=\dfrac{PC}{AC}\\
\qquad \dfrac{1}{2}= \dfrac{PC}{AC}\\
\qquad PC=\frac{1}{2}AC,[/tex]
ou seja, a área máxima ocorre quando [tex]P[/tex] é o ponto médio do lado [tex]\overline{AC}.[/tex]
Solução elaborada pelos Moderadores do Blog.

Lembretes para a Solução 2
[tex]{\color{#800000}(4)}[/tex] A razão entre as áreas de dois triângulos semelhantes é o quadrado da razão de semelhança.
[tex]{\color{#800000}(5)}[/tex] Dados [tex]n[/tex] números reais não negativos, indique por [tex]MA[/tex] sua média aritmética e por [tex]MG[/tex] sua média geométrica. Um resultado importantíssimo é a desigualdade [tex]MA\geqslant MG[/tex]. Para aprender mais, dê uma passadinha pela Sala de Estudo Médias e Desigualdades.
Solução 2
Observe que os triângulos [tex]ABC[/tex], [tex]AMP[/tex] e [tex]PNC[/tex] são semelhantes entre si, uma vez que possuem os lados paralelos e, portanto, os mesmos ângulos internos.
Seja [tex]a=AP[/tex] e [tex]c=PC[/tex]. A razão de semelhança entre [tex]AMP[/tex] e [tex]ABC[/tex] é dada por [tex]\dfrac{a}{a+c}[/tex], enquanto a razão de semelhança entre [tex]PNC[/tex] e [tex]ABC[/tex] é dada por [tex]\dfrac{c}{a+c}[/tex].
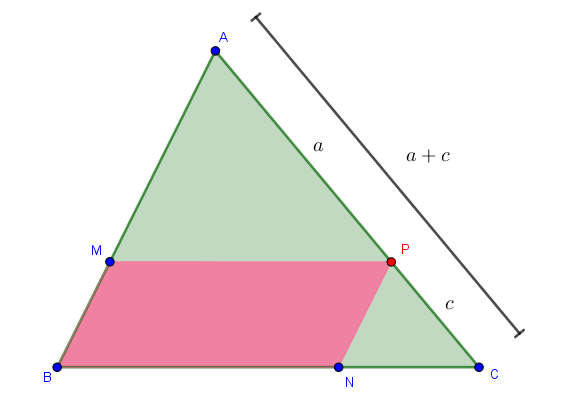
Logo, sendo [tex]S[/tex] a área de [tex]ABC[/tex], pelo Lembrete [tex]{\color{#800000}(4)}[/tex],
- a área de [tex]AMP[/tex] é [tex]\bigg(\dfrac{a}{a+c}\bigg)^2S[/tex];
- a área de [tex]PNC[/tex] é [tex]\bigg(\dfrac{c}{a+c}\bigg)^2S[/tex].
Assim, a área [tex]A_p[/tex] do paralelogramo é dada por
[tex]\qquad A_p=S-\bigg[\bigg(\dfrac{a}{a+c}\bigg)^2S+\bigg(\dfrac{c}{a+c}\bigg)^2S\bigg][/tex]
[tex]\qquad A_p=S-\bigg[\dfrac{a^2}{(a+c)^2}S+\dfrac{c^2}{(a+c)^2}S\bigg][/tex]
[tex]\qquad A_p=S-\dfrac{a^2+c^2}{a^2+2ac+c^2}S[/tex]
[tex]\qquad A_p=S\cdot \bigg(1-\dfrac{a^2+c^2}{a^2+2ac+c^2}\bigg)[/tex]
[tex]\qquad A_p=S\cdot \dfrac{\cancel{a^2}+2ac+\bcancel{c^2}-\cancel{a^2}-\bcancel{c^2}}{a^2+2ac+c^2}[/tex]
[tex]\qquad A_p=S\cdot \dfrac{2ac}{(a+c)^2}[/tex]
Como queremos a área máxima do paralelogramo, precisamos maximizar [tex]\dfrac{2ac}{(a+c)^2}[/tex]. Vejamos.
Pela Desigualdade [tex]MA\geqslant MG[/tex] (Lembrete [tex]{\color{#800000}(5)}[/tex]), veja que [tex]\dfrac{a+c}{2}\geqslant \sqrt{ac}[/tex], donde
[tex]\qquad \dfrac{(a+c)^2}{4}\geqslant ac\qquad [/tex] e [tex]\qquad 2ac\leqslant (a+c)^2\cdot \dfrac{1}{2}[/tex],
isto é,
[tex]\qquad \dfrac{2ac}{(a+c)^2}\leqslant \dfrac{1}{2}[/tex], ocorrendo a igualdade se, e somente se, [tex]a=c[/tex].
Portanto, a área máxima do paralelogramo é [tex]\dfrac{1}{2}S[/tex] (metade da área do triângulo [tex]ABC[/tex]) e ocorre quando [tex]P[/tex] é o ponto médio de [tex]\overline{AC}[/tex].
Solução elaborada pelos Moderadores do Blog.
Um applet para ilustrar. . .
Você pode visualizar o resultado demonstrado simulando vários triângulos [tex]ABC[/tex] e observando, em cada um, as áreas de vários paralelogramos [tex]BNPM.[/tex] Para isso é só esperar o aplicativo carregar completamente e seguir as instruções que irão aparecer.
Para retornar à configuração inicial, clique nas setinhas que aparecem no canto superior direito do aplicativo.
OBMEP_nzm, criado com o GeoGebra