.Problema para ajudar na escola: Duas lúnulas coloridas

Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)

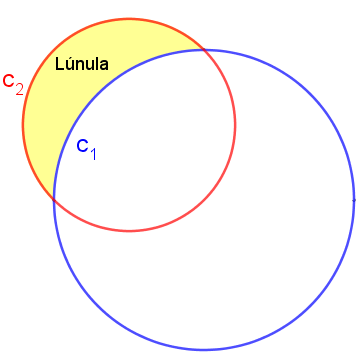
Informalmente, chamamos de lúnula a figura geométrica limitada por dois arcos circulares de raios distintos.
A figura a seguir mostra uma lúnula definida por um arco da circunferência [tex]\textcolor{blue}{C_1}[/tex] e um arco da circunferência [tex]\textcolor{red}{C_2}.[/tex]

Segundo a História da Matemática, as lúnulas foram objeto de estudo do matemático grego Hipócrates de Chios/Quios, nascido na ilha de Chios, do século V A.C. (Não confunda o Hipócrates das lúnulas com outro: Hipócrates de Cos, conhecido como o Pai da Medicina Moderna.)

(a) A figura abaixo mostra um triângulo retângulo de catetos [tex]6 \, \text{cm}\, [/tex]e [tex] \, 8 \, \text{cm}[/tex] e três semicircunferências tendo os lados desse triângulo como diâmetros.

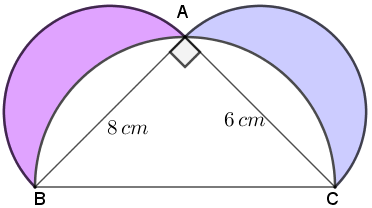
Determine a soma das áreas das duas lúnulas coloridas.

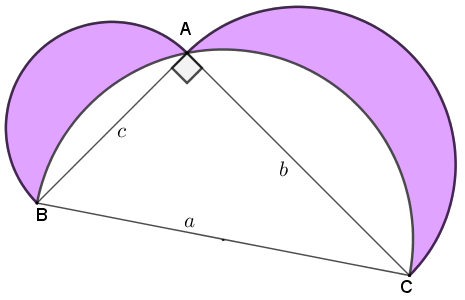
(b) Tente estabelecer o caso geral da soma das áreas de duas lúnulas definidas por arcos cujos diâmetros são os lados de um triângulo retângulo de catetos com comprimentos [tex]b \, [/tex] e [tex] \, c[/tex] e hipotenusa medindo [tex] \, a.[/tex]

Solução

(a) Se denominarmos as áreas das duas lúnulas por [tex]L_1[/tex] e [tex]L_2[/tex], conforme mostra a figura abaixo, observamos que a área de cada lúnula é a área do respectivo semicírculo que a define menos a respectiva área dentre as que denotamos por [tex]S_1[/tex] e [tex]S_2[/tex]. Como a área do semicírculo de diâmetro [tex]\overline{AB}[/tex] é [tex]\dfrac{\pi\, 4^2}{2}=8\pi[/tex] e a área do semicírculo de diâmetro [tex]\overline{AC}[/tex] é [tex]\dfrac{\pi\, 3^2}{2}=\dfrac{9\pi}{2}[/tex], segue que:

[tex]\boxed{ L_1=8\pi-S_1}\qquad [/tex] e [tex]\qquad \qquad \boxed{L_2=\dfrac{9\pi}{2}-S_2} \, .\qquad \qquad \textcolor{#800000}{(i)}[/tex]

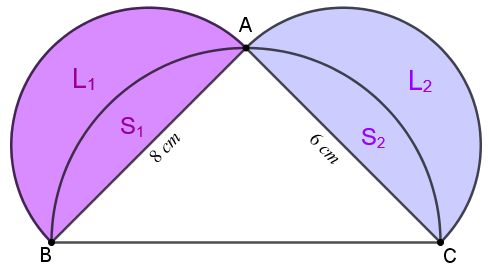
Assim, por [tex]\textcolor{#800000}{(i)}[/tex], a soma das áreas das duas lúnulas coloridas é

[tex]\boxed{ L_1+L_2=\left(8\pi+\dfrac{9\pi}{2}\right)-\left(S_1+S_2\right)} \, \qquad \qquad \textcolor{#800000}{(ii)}[/tex]

e, portanto, precisamos determinar a soma de áreas [tex]S_1+S_2[/tex]. A próxima figura indica que a soma [tex]S_1+S_2[/tex] é dada pela diferença entre a área do semicírculo de diâmetro [tex]\overline{BC}[/tex] e a área do triângulo retângulo [tex]ABC.[/tex]
O Teorema de Pitágoras nos permite concluir que o comprimento [tex]h[/tex] da hipotenusa do triângulo [tex]ABC[/tex] é tal que [tex]h^2=6^2+8^2=100[/tex], donde segue que [tex]h=10 \, \text{cm}.[/tex]

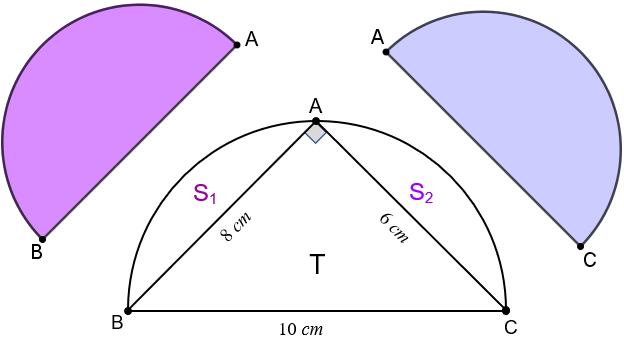
Com isso, segue que [tex]S_1+S_2=\dfrac{\pi\, 5^2}{2}-T[/tex] e, como o triângulo [tex]ABC[/tex] é retângulo, [tex]T= \dfrac{6 \times 8}{2}=24.[/tex] Portanto:

[tex]\boxed{ S_1+S_2=\dfrac{25\, \pi}{2}-24}.\qquad \qquad \textcolor{#800000}{(iii)}[/tex]

Finalmente, por [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex], obtemos que
[tex]\qquad L_1+L_2=\left(8\pi+\dfrac{9\pi}{2}\right)-\left(S_1+S_2\right)[/tex]
[tex]\qquad L_1+L_2=\left(\dfrac{25\, \pi}{2}\right)-\left(\dfrac{25\, \pi}{2}-24\right)[/tex]
[tex]\qquad L_1+L_2=24\,\text{cm}^2.[/tex]
Logo, a soma das áreas das duas lúnulas coloridas é [tex] \, \fcolorbox{black}{#eee0e5}{$ 24\,\text{cm}^2$} \, .[/tex]

(b) À primeira vista, é surpreendente que uma área que envolva áreas de semicírculos e, consequentemente, o número [tex]\pi[/tex], seja um número racional; no nosso caso, até inteiro. Mais ainda, note que a soma das áreas em questão é igual à área do triângulo retângulo, cujos lados definiram as duas lúnulas.

Coincidência?

Vamos mostrar que não. Para isso repetiremos o raciocínio que desenvolvemos no item (a), para um triângulo retângulo genérico de lados [tex]a, \, b, \, c.[/tex]

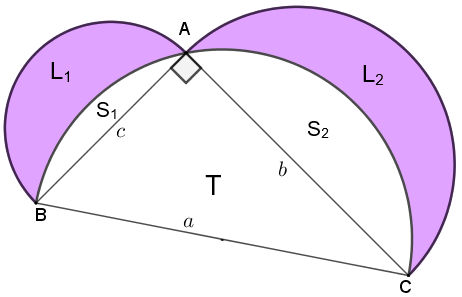
Observe que:

• Área do semicírculo de diâmetro [tex] \overline{AB}: L_1+S_1[/tex]

[tex]\qquad \qquad \dfrac{\pi\left(\frac{c}{2}\right)^2}{2}=L_1+S_1 \qquad \textcolor{#800000}{(i)}[/tex]

• Área do semicírculo de diâmetro [tex] \overline{AC}: L_2+S_2[/tex]

[tex]\qquad \qquad \dfrac{\pi\left(\frac{b}{2}\right)^2}{2}=L_2+S_2 \qquad \textcolor{#800000}{(ii)}[/tex]

• Área do triângulo [tex] ABC[/tex]

[tex]\qquad \qquad\dfrac{b \times c}{2} =T\qquad \textcolor{#800000}{(iii)}[/tex]

Somando as equações [tex]\textcolor{#800000}{(i)}[/tex], [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex], segue que:
[tex]\qquad \qquad \dfrac{\pi\left(\frac{c}{2}\right)^2}{2}+\dfrac{\pi\left(\frac{b}{2}\right)^2}{2}+\dfrac{b \times c}{2}=\left(L_1+S_1\right)+\left(L_2+S_2\right)+T[/tex]
[tex]\qquad \qquad \dfrac{\pi}{2} \left(\left(\dfrac{c}{2}\right)^2+\left(\dfrac{b}{2}\right)^2\right)+\dfrac{b \times c}{2}=\left(L_1+L_2\right)+\left(S_1+S_2+T\right)[/tex]
[tex]\qquad \qquad \dfrac{\pi}{8} \left(b^2+c^2\right)+\dfrac{b \times c}{2}=\left(L_1+L_2\right)+\left(S_1+S_2+T\right).\qquad \qquad \textcolor{#800000}{(iv)}[/tex]
Como o triângulo [tex] ABC[/tex] é retângulo, o Teorema de Pitágoras nos garante que [tex]b^2+c^2=a^2[/tex]. Assim, segue de [tex]\textcolor{#800000}{(iv)}[/tex] que:
[tex]\qquad \qquad \dfrac{\pi}{8} a^2+\dfrac{b \times c}{2}=\left(L_1+L_2\right)+\left(S_1+S_2+T\right).\qquad \qquad \textcolor{#800000}{(v)}[/tex]
Mas [tex]S_1+S_2+T[/tex] é a área do semicírculo de diâmetro [tex]\overline{BC}[/tex]; assim, [tex]S_1+S_2+T=\dfrac{\pi\, \left(\frac{a}{2}\right)^2}{2}=\dfrac{\pi}{8} a^2[/tex] e, por [tex]\textcolor{#800000}{(v)}[/tex], temos que:
[tex]\qquad \qquad \dfrac{\pi}{8} a^2+\dfrac{b \times c}{2}=\left(L_1+L_2\right)+\underbrace{\left(S_1+S_2+T\right)}_{\dfrac{\pi}{8} a^2}[/tex]

[tex]\qquad \qquad \cancel{\dfrac{\pi}{8} a^2}+\dfrac{b \times c}{2}=\left(L_1+L_2\right)+\cancel{\dfrac{\pi}{8} a^2}.[/tex]
Portanto,[tex]\dfrac{b \times c}{2}=L_1+L_2[/tex] e, de fato, a soma das áreas das lúnulas em questão é a área do triângulo [tex]ABC.[/tex]

Solução elaborada pelos Moderadores do Blog.