Problema
(Indicado a partir do 1º ano do E. M.)
Mariana está produzindo asas de morcegos para sua festa de Halloween. Para isso, Mariana traça em pedaços retangulares de papel, com [tex]4\ cm[/tex] de largura e [tex]3\ cm[/tex] de comprimento, dois segmentos de reta que se intersectam, formando assim os dois triângulos que definem as asas de um morcego.
A construção de um par de asas está sendo realizada de acordo com o esquema reproduzido na imagem abaixo, no qual [tex]AFED[/tex] representa a folha retangular e [tex]\overline{CF}[/tex] e [tex]\overline{BE}[/tex] são os segmentos que definem um par de asas triangulares.
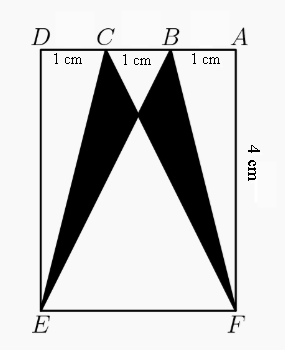
Calcule a área de um par de asas de morcego.

Lembretes
(1) Se duas retas paralelas são intersectadas por uma transversal, então os pares de ângulos alternos internos que essa transversal define são congruentes. (Precisa relembrar estes conceitos? Dê uma passadinha nesta Sala.)
(2) Caso de Semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes. (Há uma Sala de Ajuda sobre esse tema no Blog!)
Solução
No esquema utilizado por Mariana, seja [tex]G[/tex] o ponto de interseção dos segmentos [tex]\overline{CF}[/tex] e [tex]\overline{BE}[/tex], conforme abaixo indicado.
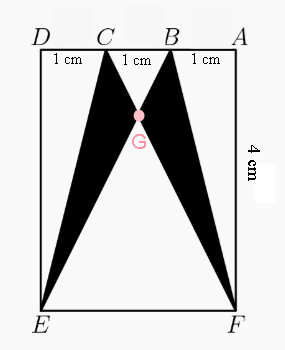
Para calcularmos a área de um par de asas, basta calcularmos a área do trapézio [tex]CBFE[/tex] e retirarmos dela as áreas dos triângulos [tex]CBG[/tex] e [tex]EFG[/tex].
- A área [tex]A_t[/tex] do trapézio [tex]CBFE[/tex] é dada por [tex]\boxed{A_t=\dfrac{(3+1)\times 4}{2}=8 \ cm^2} \, .[/tex]
- Para obtermos as áreas dos triângulos [tex]CBG[/tex] e [tex]EFG[/tex], observe inicialmente que esses triângulos são semelhantes pelo Lembrete (2) .
-
Com efeito os segmentos [tex]\overline{AD} [/tex] e [tex]\overline{EF} [/tex]são paralelos e a reta transversal [tex]CF[/tex] define os ângulos alternos internos [tex]\hat{ACF}[/tex] e [tex]\hat{CFE}[/tex] que, pelo Lembrete (1), são congruentes. Da mesma forma, em função da reta transversal [tex]BE[/tex], podemos concluir que os ângulos [tex]\hat{DBE}[/tex] e [tex]\hat{BEF}[/tex] são congruentes.
Podemos então afirmar que a razão entre os comprimentos das bases dos triângulos [tex]CBG[/tex] e [tex]EFG[/tex] é igual à razão dos comprimentos das respectivas alturas; assim, segue que:
[tex]\qquad \dfrac{1}{3}=\dfrac{h_{CBG}}{h_{EFG}} \\
\qquad h_{EFG}=3h_{CBG}.\\
\, \, [/tex]
Utilizando a igualdade [tex] h_{EFG}+h_{CBG}=4,[/tex] obtemos também:
[tex]\qquad 3h_{CBG}+h_{CBG}=4[/tex]
[tex]\qquad 4h_{CBG}=4[/tex]
[tex]\qquad h_{CBG}=1\ cm \, [/tex] e [tex] \, h_{EFG}=3\times 1 =3 \ cm.[/tex]
Assim, já podemos calcular as áreas dos triângulos [tex]CBG[/tex] e [tex]EFG[/tex]:
[tex] \, \boxed{A_{CBG}=\dfrac{1\times 1}{2}=\dfrac{1}{2}\ cm^2} \, \, \, \, [/tex] e [tex] \, \, \, \, \boxed{A_{EFG}=\dfrac{3\times 3}{2}=\dfrac{9}{2} \ cm^2} \, .[/tex]
Finalmente, podemos concluir que a área de um par de asas de morcego é dada por:
[tex]\qquad \, \fcolorbox{black}{#eee0e5}{$\begin{align} A_{asa}&=A_t-A_{CBG}-A_{EFG}\\
&=8-\dfrac{1}{2}-\dfrac{9}{2}\\
&=3 \ cm^2\end{align}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
