Problema
(Indicado a partir do 9º ano do E. F.)
Na figura abaixo, a reta que contém os pontos [tex]A[/tex] e [tex]B[/tex] é paralela à reta que contém [tex]C[/tex] e [tex]D[/tex].
Determine a medida do ângulo [tex]\alpha[/tex], sabendo que [tex]PB = 2 \cdot AC[/tex].
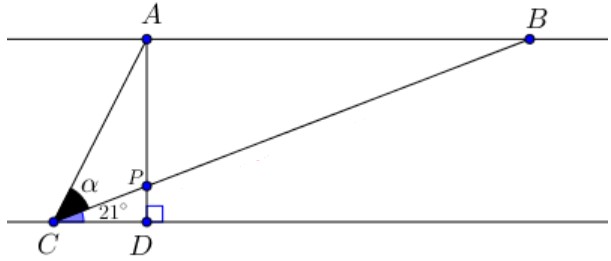
Notação: Dados dois pontos distintos [tex]X \, [/tex] e [tex] \, Y \, [/tex], denotaremos o segmento que eles definem por [tex]\overline {XY} [/tex] e o comprimento desse segmento por [tex]XY[/tex].

Lembretes
(1) Ângulos alternos internos definidos por retas paralelas têm a mesma medida. (Se você não se lembra dos ângulos alternos internos, clique AQUI.)
(2) A medida de um ângulo externo a um triângulo qualquer é a soma das medidas dos ângulos internos do triângulo que não são adjacentes a ele.
(3) A mediana de um triângulo retângulo, com vértice no ângulo reto, mede a metade da hipotenusa.
Solução
Inicialmente podemos explorar a figura dada no problema e descobrir que:
- a medida do ângulo [tex]A\hat{B}P[/tex] é [tex]21^\circ[/tex], já que [tex]A\hat{B}P[/tex] e [tex]B\hat{C}D[/tex] são ângulos alternos internos;
- o triângulo [tex] ABP[/tex] é retângulo em [tex]A[/tex];
- além disso, se [tex]AC=x[/tex], então [tex]PB = 2 \cdot x[/tex].
Destacaremos na próxima figura o ponto [tex]M[/tex], ponto médio de [tex]\overline{PB}[/tex].
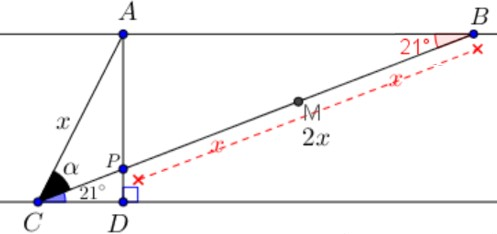
Agora, lembrando que a mediana de um triângulo retângulo, com vértice no ângulo reto, mede a metade da hipotenusa, podemos concluir que [tex]AM=x[/tex]. Dessa forma, o [tex]\triangle AMB[/tex] é isósceles, com ângulos da base medindo [tex]21^\circ[/tex].
Com mais essa informação, podemos aplicar o teorema do ângulo externo no triângulo [tex]ABM[/tex] e concluir que a medida do ângulo [tex]A\hat{M}C[/tex] é [tex]42^\circ \, .[/tex]
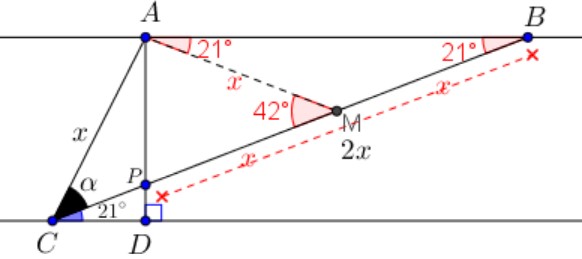
Por fim, note que [tex]\triangle AMC[/tex] também é um triângulo isósceles, com [tex]\overline{AC} \equiv \overline{AM}[/tex].
Portanto, [tex]\fcolorbox{black}{#eee0e5}{$\alpha=42^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
