Problema
(Indicado a partir do 9º ano do E. F.)
Num triângulo [tex]OAB[/tex], retângulo em [tex]O[/tex], tem-se [tex]OA = a[/tex] e [tex]OB = b[/tex].
É dado que existem os pontos [tex]P[/tex] em [tex]\overline{OA}[/tex] e [tex]Q[/tex] em [tex]\overline{OB}[/tex] tais que [tex]AP = PQ = QB = x[/tex].
Nessas condições, calcule o valor de [tex]x[/tex] em função de [tex]a[/tex] e [tex]b[/tex].
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].

Ajuda
Nesta solução, vamos utilizar o Teorema de Pitágoras.
Caso precisem de ajuda com este tema, não deixem de dar uma olhada na Sala para Leitura Reencontrando triângulos retângulos.
Bom proveito, pessoal!
Solução
Observe a figura de referência abaixo.
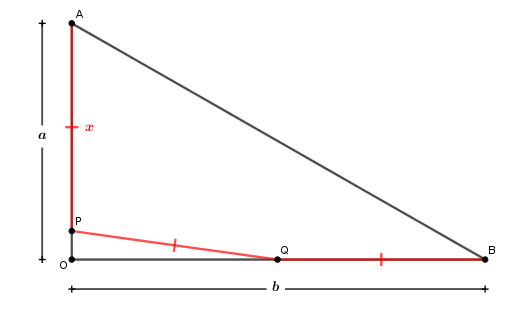
Note que o triângulo [tex]OPQ[/tex] também será retângulo em [tex]O[/tex]. Assim, seus lados obedecem à Relação de Pitágoras, isto é, temos
[tex]OP^2+OQ^2=PQ^2 \, [/tex], donde:
[tex]\qquad (a-x)^2+(b-x)^2=x^2[/tex]
[tex]\qquad a^2-2ax\cancel{+x^2}+b^2-2bx+x^2=\cancel{x^2}[/tex]
[tex]\qquad a^2-2ax+b^2-2bx+x^2=0[/tex]
[tex]\qquad x^2-(2a+2b)x+(a^2+b^2)=0.\qquad \textcolor{#800000}{(i)}[/tex]
Veja que a igualdade [tex]\textcolor{#800000}{(i)}[/tex] é uma equação do segundo grau em [tex]x[/tex]. Para descobrirmos [tex]x[/tex], podemos utilizar a fórmula de resolução desse tipo de equação:
[tex]\qquad x=\dfrac{(2a+2b)\pm\sqrt{\left(-(2a+2b)\right)^2-4\cdot 1\cdot (a^2+b^2)}}{2\cdot1}[/tex]
[tex]\qquad x=\dfrac{2(a+b)\pm\sqrt{\cancel{4a^2}+8ab+\bcancel{4b^2}\cancel{-4a^2}\bcancel{-4b^2}}}{2}[/tex]
[tex]\qquad x=\dfrac{2(a+b)\pm\sqrt{8ab}}{2}[/tex]
[tex]\qquad x=\dfrac{\cancel{2}(a+b)\pm\cancel{2}\sqrt{2ab}}{\cancel{2}}[/tex]
[tex]\qquad x=a+b\pm\sqrt{2ab}.[/tex]
Assim, a equação [tex]\textcolor{#800000}{(i)}[/tex] tem duas soluções: [tex]x_1=a+b+\sqrt{2ab}\quad[/tex] e [tex]\quad x_2=a+b-\sqrt{2ab}.[/tex]
Mas perceba que [tex]x\lt a[/tex], pois o ponto [tex]P[/tex] está entre os pontos [tex]O[/tex] e [tex]A[/tex]. Então, obviamente, [tex]x\lt a+b[/tex], e portanto devemos diminuir [tex]\sqrt{2ab}[/tex] de [tex]a+b[/tex] para encontrar [tex]x[/tex], não somar.
Portanto [tex] \, \fcolorbox{black}{#eee0e5}{$x=a+b-\sqrt{2ab}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
