.Diagrama de Venn – Problemas propostos – Clubes de Matemática da OBMEP

Diagramas de Venn – Problemas propostos

Raciocínio Lógico

Problema proposto 1: (FCC/2012 – Concurso TCE-SP – Analista de Fiscalização Financeira (Administração))
Todos os jogadores são rápidos. Jorge é rápido. Jorge é estudante. Nenhum jogador é estudante.
Supondo as frases verdadeiras pode-se afirmar que:

[tex](A)[/tex] a intersecção entre o conjunto dos jogadores e o conjunto dos rápidos é vazia.
[tex](B)[/tex] a intersecção entre o conjunto dos estudantes e o conjunto dos jogadores não é vazia.
[tex](C)[/tex] Jorge pertence ao conjunto dos jogadores e dos rápidos.
[tex](D)[/tex] Jorge não pertence à intersecção entre os conjuntos dos estudantes e o conjunto dos rápidos.
[tex](E)[/tex] Jorge não pertence à intersecção entre os conjuntos dos jogadores e o conjunto dos rápidos.

Problema proposto 2: (PUC-RJ)
Um levantamento socioeconômico entre os habitantes de uma cidade revelou que, exatamente:

[tex]17\%[/tex] têm casa própria;
[tex]22\%[/tex] têm automóvel;
[tex]8\%[/tex] têm casa própria e automóvel.

Qual o percentual dos que não têm casa própria nem automóvel?

Problema proposto 3: (VUNESP/2011 – Concurso TJM-SP – Analista de Sistemas (Judiciário))
Neste grupo de pessoas, usar só chapéu ou só relógio, nem pensar. Tampouco usar óculos, chapéu e relógio ao mesmo tempo. Quinze pessoas usam óculos e chapéu ao mesmo tempo. Usam chapéu e relógio, simultaneamente, o mesmo número de pessoas que usam apenas os óculos. Uma pessoa usa óculos e relógio ao mesmo tempo.
Esse grupo é formado por 40 pessoas e essas informações são suficientes para afirmar que nesse grupo o número de pessoas que usam óculos é

[tex]\qquad(A)\, 20. \qquad(B)\, 22. \qquad(C)\, 246. \qquad(D)\, 26. \qquad(E)\, 28.[/tex]

Problema proposto 4: (UNICAMP-2009)
Três candidatos A, B e C concorrem à presidência de um clube. Uma pesquisa apontou que, dos sócios entrevistados, [tex]150[/tex] não pretendem votar. Dentre os entrevistados que estão dispostos a participar da eleição, [tex]40[/tex] sócios votariam apenas no candidato A, [tex]70[/tex] votariam apenas em B, e [tex]100[/tex] votariam apenas no candidato C. Além disso, [tex]190[/tex] disseram que não votariam em A, [tex]110[/tex] disseram que não votariam em C, e [tex]10[/tex] sócios estão na dúvida e podem votar tanto em A como em C, mas não em B. Finalmente, a pesquisa revelou que [tex]10[/tex] entrevistados votariam em qualquer candidato.
Com base nesses dados, pergunta-se:
a) Quantos sócios entrevistados estão em dúvida entre votar em B ou em C, mas não votariam em A? Dentre os sócios consultados que pretendem participar da eleição, quantos não votariam em B?
b) Quantos sócios participaram da pesquisa? Suponha que a pesquisa represente fielmente as intenções de voto de todos os sócios do clube. Escolhendo um sócio ao acaso, qual a probabilidade de que ele vá participar da eleição mas ainda não tenha se decidido por um único candidato?

Problema proposto 5: (FGV – SP)
Em uma pesquisa de mercado foram entrevistadas várias pessoas acerca de suas preferências em relação a três produtos, A, B e C. Os resultados da pesquisa indicaram que:

[tex]210[/tex] pessoas compram o produto A
[tex]210[/tex] pessoas compram o produto B
[tex]250[/tex] pessoas compram o produto C
[tex]20[/tex] pessoas compram os três produtos
[tex]100[/tex] pessoas não compram nenhum dos três produtos
[tex]60[/tex] pessoas compram os produtos A e B
[tex]70[/tex] pessoas compram os produtos A e C
[tex]50[/tex] pessoas compram os produtos B e C.

Quantas pessoas foram entrevistadas?

Problema proposto 6: (PUC-PR-2003)
Em uma pesquisa feita com [tex]120[/tex] empregados de uma firma, verificou-se o seguinte:

Qual a porcentagem dos empregados que não se enquadram em nenhuma das situações anteriores?

[tex]\qquad(A)\,25\%. \qquad(B)\, 30\%. \qquad(C)\, 35\%. \qquad(D)\, 40\%. \qquad(E)\, 45\%.[/tex]

Problema proposto 7: (Vunesp-2000)
Um estudo de grupos sanguíneos humanos realizado com [tex]1000[/tex] pessoas (sendo [tex]600[/tex] homens e [tex]400[/tex] mulheres) constatou que [tex]470[/tex] pessoas tinham o antígeno A, [tex]230[/tex] pessoas tinham o antígeno B e [tex]450[/tex] pessoas não tinham nenhum dos dois.
Determine:
a) o número de pessoas que têm os antígenos A e B simultaneamente;
b) supondo independência entre sexo e grupo sanguíneo, a probabilidade de que uma pessoa do grupo, escolhida ao acaso, seja homem e tenha os antígenos A e B simultaneamente.

Problema proposto 8: (ITA-2002)
Sejam [tex]A[/tex] um conjunto com [tex]8[/tex] elementos e [tex]B[/tex] um conjunto tal que [tex]A \cup B[/tex] contenha [tex]12[/tex] elementos. Então, o número de elementos de [tex] P(B \setminus A) \cup P(\varnothing)[/tex] é igual a

[tex]\qquad(A)\,8. \qquad(B)\, 16. \qquad(C)\, 20. \qquad(D)\, 17. \qquad(E)\, 9.[/tex]

OBS.:
(i) Se [tex]X[/tex] é um conjunto, [tex] P(X)[/tex] denota o conjunto de todos os subconjuntos de [tex]X[/tex].
(ii) [tex]A \setminus B = \{x\in A; x \not\in B\}. [/tex]

Problema proposto 9: (UFMG-2003)
Em uma pesquisa de opinião, foram obtidos estes dados:

40% dos entrevistados leem o jornal A.
55% dos entrevistados leem o jornal B.
35% dos entrevistados leem o jornal C.
12% dos entrevistados leem os jornais A e B.
15% dos entrevistados leem os jornais A e C.
19% dos entrevistados leem os jornais B e C.
7% dos entrevistados leem os três jornais.
135 pessoas entrevistadas não leem nenhum dos três jornais.

Considerando-se estes dados, é CORRETO afirmar que o número total de entrevistados foi:

[tex]\qquad(A)\,1200. \qquad\qquad (B)\, 1500. \qquad\qquad (C)\, 1250. \qquad\qquad (D)\, 1350.[/tex]

Problema proposto 10: (FGV-2004)
Uma pesquisa com três marcas concorrentes de refrigerantes, A, B e C, mostrou que 60% das pessoas entrevistadas gostam de A,

50% gostam de B,
57% gostam de C,
35% gostam de A e C,
18% gostam de A e B,
24% gostam de B e C,
2% gostam das três marcas,
o restante das pessoas não gosta de nenhuma das três.

Sorteando-se aleatoriamente uma dessas pessoas entrevistadas, a probabilidade de que ela goste de uma única marca de refrigerante ou não goste de marca alguma é de

[tex]\qquad(A)\,16\%. \qquad(B)\, 17\%. \qquad(C)\, 20\%. \qquad(D)\, 25\%. \qquad(E)\, 27\%.[/tex]

Problema proposto 11: (EPCAR-2003)
Numa turma de 31 alunos da EPCAR, foi aplicada uma Prova de Matemática valendo 10 pontos no dia em que 2 alunos estavam ausentes. Na prova, constavam questões subjetivas: a primeira, sobre conjuntos; a segunda, sobre funções e a terceira, sobre geometria plana. Sabe-se que dos alunos presentes

nenhum tirou zero;
11 acertaram a segunda e a terceira questões;
15 acertaram a questão sobre conjuntos;
1 aluno acertou somente a parte de geometria plana,
e 7 alunos acertaram apenas a questão sobre funções.

É correto afirmar que o número de alunos com grau máximo igual a 10 foi

[tex]\qquad(A)\, 4. \qquad\qquad (B)\, 5. \qquad\qquad (C)\, 6. \qquad\qquad (D)\, 7.[/tex]

Problema proposto 12: (UFRJ-1999)
Uma amostra de 100 caixas de pílulas anticoncepcionais fabricadas pela Nascebem S.A. foi enviada para a fiscalização sanitária.
No teste de qualidade, 60 foram aprovadas e 40 reprovadas, por conterem pílulas de farinha. No teste de quantidade, 74 foram aprovadas e 26 reprovadas, por conterem um número menor de pílulas que o especificado.
O resultado dos dois testes mostrou que 14 caixas foram reprovadas em ambos os testes.
Quantas caixas foram aprovadas em ambos os testes?

Problema proposto 13: (AFA-1998)
Em um grupo de [tex]n[/tex] cadetes da Aeronáutica, 17 nadam, 19 jogam basquetebol, 21 jogam voleibol, 5 nadam e jogam basquetebol, 2 nadam e jogam voleibol, 5 jogam basquetebol e voleibol e 2 fazem os três esportes.
Qual o valor de [tex]n[/tex] , sabendo-se que todos os cadetes desse grupo praticam pelo menos um desses esportes?

[tex]\qquad(A)\,31. \qquad\qquad (B)\, 37. \qquad\qquad (C)\, 47. \qquad\qquad (D)v 51.[/tex]

Problema proposto 14: (ENEM-2008) A vida na rua como ela é
O Ministério do Desenvolvimento Social e Combate à Fome (MDS) realizou, em parceria com a ONU, uma pesquisa nacional sobre a população que vive na rua, tendo sido ouvidas 31.922 pessoas em 71 cidades brasileiras.
Nesse levantamento, constatou-se que a maioria dessa população sabe ler e escrever (74%), que apenas 15,1% vivem de esmolas e que, entre os moradores de rua que ingressaram no ensino superior, 0,7% se diplomou. Outros dados da pesquisa são apresentados nos quadros abaixo.

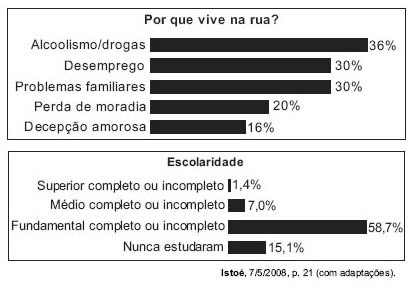
No universo pesquisado, considere que P seja o conjunto das pessoas que vivem na rua por motivos de alcoolismo/drogas e Q seja o conjunto daquelas cujo motivo para viverem na rua é a decepção amorosa.
Escolhendo-se ao acaso uma pessoa no grupo pesquisado e supondo-se que seja igual a 40% a probabilidade de que essa pessoa faça parte do conjunto P ou do conjunto Q, então a probabilidade de que ela faça parte do conjunto interseção de P e Q é igual a

[tex]\qquad(A)\,12\%. \qquad (B)\, 16\%. \qquad(C)\, 20\%. \qquad(D)\, 36\%. \qquad(E)\, 52\%.[/tex]

Problema proposto 15: (AFA-1998)
Entrevistando 100 oficiais da AFA, descobriu-se que 20 deles pilotam a aeronave TUCANO, 40 pilotam o helicóptero ESQUILO e 50 não são pilotos.
Dos oficiais entrevistados, quantos pilotam o TUCANO e o ESQUILO?

[tex]\qquad (A)\,5. \qquad\qquad (B)\, 10. \qquad\qquad (C)\, 15. \qquad\qquad (D)\, 20.[/tex]

Problema proposto 16:
Em uma cidade foi feita uma pesquisa sobre os meios de transporte mais usados entre ônibus, metrô e moto. Foram obtidas as seguintes respostas dos 3.200 entrevistados:
– 1950 utilizam o metrô;
– 400 utilizam moto;
– 1500 utilizam ônibus;
– 800 utilizam ônibus e metrô;
– e nenhum dos entrevistados que utiliza moto utiliza ônibus ou metrô.
Assim:
(a) Quantas pessoas entrevistadas utilizam apenas o metrô?
(b) Quantas pessoas entrevistadas utilizam exatamente dois meios de transportes?

Problema proposto 17: (UFAL – adaptado)
O resultado de uma pesquisa mostrou que, em um grupo de 77 jovens, há:

Com relação a esse grupo, quais das afirmações abaixo são verdadeiras?

(01) O número de rapazes é 50.
(02) O número de rapazes que não trabalham nem estudam é 12.
(03) O número de moças que trabalham e não estudam é 9.
(04) O número de rapazes que trabalham e estudam é 9.
(05) O número de moças que estudam e não trabalham é 4.

Tente resolver os problemas propostos e, se você faz parte de um Clube fundado, não hesite: qualquer dúvida, poste-a nas Salas de Dúvidas do Fórum restrito dos Clubes.
Lembre-se de que a nossa Equipe estará lá para ajudá-lo(a)!

Equipe COM – OBMEP

Voltar para Sala de Estudos do Tema