Usando diagramas de Venn para ajudar a
entender a linguagem de conjuntos
Aqui, vamos utilizar diagramas de Venn para ilustrar e tentar entender algumas definições que aparecem de vez em quando nos nossos estudos.
I – Relação de Pertinência
Os objetos que compõem um conjunto são denominados “elementos” do conjunto em questão. A pertinência (ato de pertencer) a um conjunto é usualmente indicada pelo símbolo [tex]\in[/tex] e, a não pertinência, pelo símbolo [tex]\notin [/tex]. Assim:
► a notação [tex]x \in X[/tex] significa que "o objeto [tex]x[/tex] é elemento do conjunto [tex]X[/tex]";
► a notação [tex]b \notin B[/tex] indica que "o objeto [tex]b[/tex] não é elemento do conjunto [tex]B[/tex]".
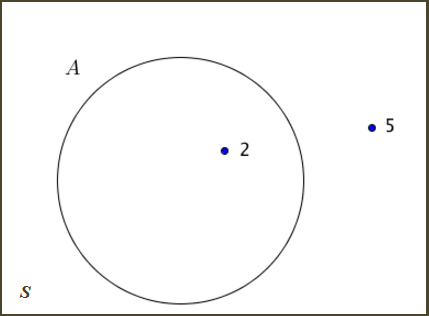
Dessa forma, utilizando a figura abaixo, podemos usar as expressões:
● [tex]2 \in A[/tex] para indicar que o número [tex]2[/tex] é elemento do conjunto [tex]A[/tex].
● [tex]5 \notin A[/tex] para indicar que o número [tex]5[/tex] não é elemento do conjunto [tex]A[/tex].
Dependendo do contexto, o símbolo [tex]\in[/tex] pode ser lido como
– “é elemento de”;
– “é membro de”;
– “está em”, “pertence a”;
e a sua negação [tex]\notin [/tex] pode ser lida como
– “não é elemento de”;
– “não é membro de”;
– “não está em”, “não pertence a”.
Particularmente, um conjunto que não tem elementos é o que definimos como um "conjunto vazio" e é representado pelo símbolo [tex]\emptyset[/tex] ou por [tex]\{ \, \, \}[/tex].
Assim, por exemplo, se [tex]S[/tex] é o conjunto dos números naturais que são pares e ímpares simultaneamente, então [tex]S=\emptyset.[/tex]
Observamos que é absolutamente incorreto utilizar [tex]\{\emptyset\}[/tex] para representar o conjunto vazio.
II – Relação de Inclusão
Se todo elemento de um conjunto [tex]A[/tex] é também elemento de um conjunto [tex]B[/tex], dizemos que [tex]A[/tex] está contido em [tex]B[/tex] (ou que [tex]A[/tex] é subconjunto de [tex]B[/tex]) e utilizamos a notação [tex]A \subset B[/tex].
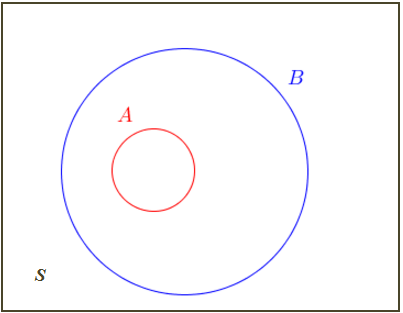
Com relação à figura acima, podemos escrever que:
► [tex]A \subset B[/tex], para indicar que [tex]A[/tex] é subconjunto de [tex]B[/tex];
► [tex]A \subset S[/tex], para indicar que [tex]A[/tex] é subconjunto de [tex]S[/tex];
► [tex]B \subset S[/tex], para indicar que [tex]B[/tex] é subconjunto de [tex]S[/tex];
► [tex]A \subset B \subset S[/tex], para indicar as três inclusões.
Se existir pelo menos um elemento de um conjunto [tex]X[/tex] que não seja elemento de um conjunto [tex]M[/tex], dizemos que [tex]X[/tex] não está contido em [tex]M[/tex] (ou que [tex]X[/tex] não é subconjunto de [tex]M[/tex]) e utilizamos a notação [tex]X \not\subset M[/tex].
Com relação à figura acima, podemos escrever que:
► [tex]B \not\subset A[/tex], para indicar que [tex]B[/tex] não é subconjunto de [tex]A[/tex];
► [tex]S \not\subset A[/tex], para indicar que [tex]S[/tex] não é subconjunto de [tex]A[/tex];
► [tex]S \not\subset B[/tex], para indicar que [tex]S[/tex] não é subconjunto de [tex]B[/tex].
III – Operações com conjuntos
Assim como podemos somar e multiplicar números, existem algumas operações que podemos fazer com conjuntos. Com isso, é possível criarmos novos conjuntos a partir de conjuntos dados utilizando essas operações, dentre as quais destacamos: a união (reunião), a interseção e a diferença. Vamos relembrar como efetuar cada uma delas e ilustrá-las com diagramas de Venn.
União (Reunião) de conjuntos
A união (reunião) de dois conjuntos [tex]A[/tex] e [tex]B[/tex] é o conjunto indicado por [tex]A \cup B[/tex] e formado por todos os elementos de [tex]A[/tex] e por todos os elementos de [tex]B[/tex].
Em símbolos:
[tex]\qquad A \cup B = \{ x \, ; \, x \in A \textrm{ ou }\, x \in B\}[/tex].
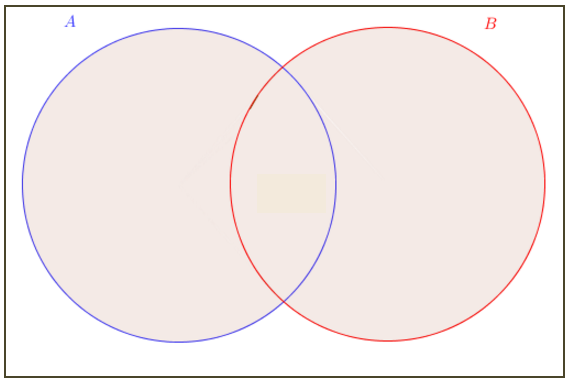
Na figura acima, [tex]A[/tex] e [tex]B[/tex] são representados pelos círculos e [tex]A \cup B[/tex] é a parte sombreada.
Nas imagens abaixo, podemos visualizar a união [tex]A \cup B[/tex] em outras situações relativas dos conjuntos [tex]A[/tex] e [tex]B.[/tex]
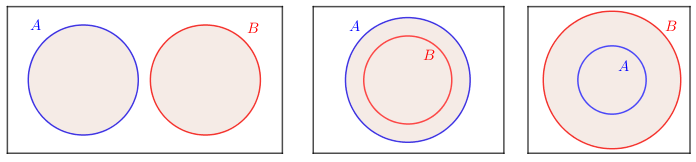
A segunda e a terceira imagens ilustram uma propriedade característica de subconjuntos:
se [tex]X[/tex] é um subconjunto de [tex]Z[/tex] ([tex]X \subset Z[/tex]), então [tex]X \cup Z=Z.[/tex]
Interseção de conjuntos
A interseção de dois conjuntos [tex]A[/tex] e [tex]B[/tex] é o conjunto indicado por [tex]A \cap B[/tex] e formado pelos elementos comuns a [tex]A[/tex] e a [tex]B[/tex].
Assim:
[tex]\qquad A \cap B = \{ x \, ; \, x \in A \text{ e } x \in B\}[/tex].
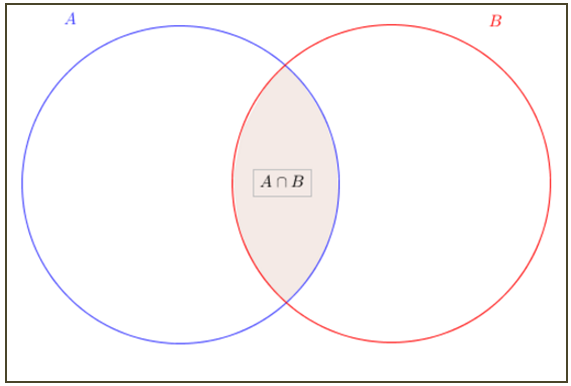
Na figura acima, [tex]A[/tex] e [tex]B[/tex] são também representados pelos círculos e [tex]A \cap B[/tex] é a parte sombreada.
Nas imagens abaixo, podemos visualizar a interseção [tex]A \cap B[/tex] em outras situações relativas dos conjuntos [tex]A[/tex] e [tex]B.[/tex]
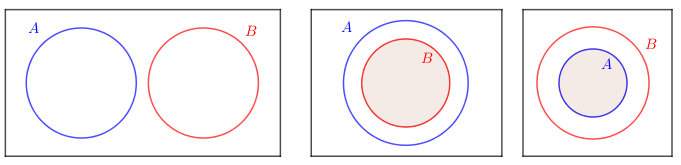
A primeira imagem ilustra uma situação importante: os conjuntos [tex]A[/tex] e [tex]B[/tex] não têm elementos em comum. Nesse caso, [tex]A \cap B=\emptyset \, [/tex] e dizemos que [tex]A[/tex] e [tex]B[/tex] são disjuntos.
A segunda e a terceira imagens ilustram mais uma propriedade característica de subconjuntos:
se [tex]X[/tex] é um subconjunto de [tex]Z[/tex] ([tex]X \subset Z[/tex]), então [tex]X \cap Z=X.[/tex]
Diferença de conjuntos
A diferença entre dois conjuntos [tex]A[/tex] e [tex]B[/tex] é o conjunto indicado por [tex]A-B[/tex] e formado pelos elementos de [tex]A[/tex] que não são elementos de [tex]B[/tex].
Dessa forma:
[tex]\qquad A–B = \{ x \, ; \, x \in A \text{ e }\, x \notin B\}[/tex].
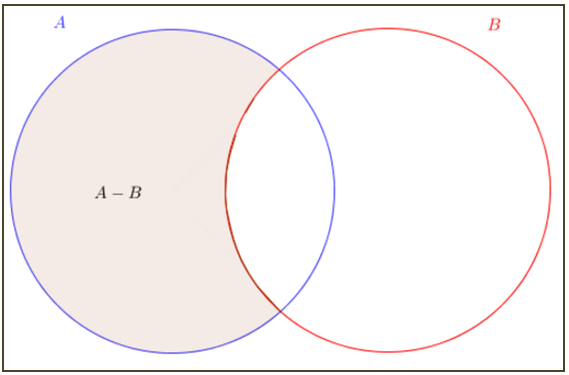
Na figura acima, uma vez mais, [tex]A[/tex] e [tex]B[/tex] são representados pelos círculos e [tex]A-B[/tex] é a parte sombreada.
Nas imagens abaixo, podemos visualizar a diferença [tex]A-B[/tex] em outras situações relativas dos conjuntos [tex]A[/tex] e [tex]B.[/tex]
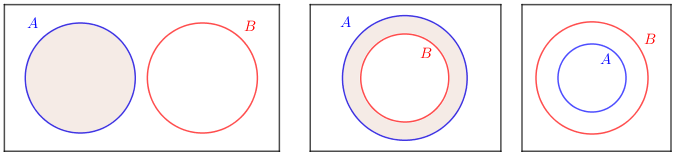
Como a diferença [tex]A-B[/tex] é, informalmente, "o que sobra de [tex]A[/tex] quando apagamos [tex]B[/tex]", a primeira e a terceira imagens acima ilustram, respectivamente, que:
se [tex]A[/tex] e [tex]B[/tex] são disjuntos ([tex]A \cap B=\emptyset \, [/tex]), então [tex]A-B=A.[/tex]
se [tex]A[/tex] é subconjunto de [tex]B[/tex]([tex]A \subset B \, [/tex]), então [tex]A-B=\emptyset.[/tex]
Quando temos [tex]A[/tex] e [tex]B[/tex] conjuntos tais que [tex]B \subset A[/tex] (segunda imagem acima), a diferença [tex]A–B[/tex] é denominada o "complementar de [tex]B[/tex], com relação a [tex]A[/tex]" e indicada por [tex]\complement_A^B [/tex]. Particularmente, se [tex]S[/tex] é um conjunto que contém todos os conjuntos envolvidos em uma determinada discussão, a diferença [tex]S-X[/tex] é dita, simplesmente, o complementar de [tex]X[/tex] e é indicada com a notação [tex]\complement X [/tex] ou [tex]\overline{X}[/tex].
Podemos utilizar diagramas de Venn para ajudar no entendimento de propriedades dessas três operações definidas. Abaixo vamos apresentar cinco dessas propriedades e ilustrar três delas.
IV – Algumas propriedades importantes
Sejam [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] conjuntos quaisquer; então valem as propriedades abaixo.
► Comutatividade da união
[tex]\qquad (A \cup B) = (B \cup A)[/tex]
► Comutatividade da interseção
[tex]\qquad (A \cap B) = (B \cap A)[/tex]
► Distributividade da união em relação à interseção
[tex]\qquad A \cup (B \cap C) = (A \cup B) \cap (A \cup C)[/tex]
► Distributividade da interseção em relação à união
[tex]\qquad A \cap (B \cup C) = (A \cap B) \cup (A \cap C)[/tex]
Se [tex]A[/tex] e [tex]B[/tex] forem subconjuntos de um conjunto [tex]S[/tex], então valem também as duas próximas propriedades.
► Leis de De Morgan
[tex]\qquad \overline{A} \cup \overline{B} = \overline{A \cap B}[/tex]
[tex]\qquad \overline{A} \cap \overline{B} = \overline{A \cup B}[/tex]
Observação: Em função das comutatividades da união e da interseção, as duas distributividades podem ser assim reescritas:
[tex]\qquad (B \cap C) \cup A = (B \cup A) \cap (C \cup A)[/tex];
[tex]\qquad (B \cup C) \cap A = (B \cap A) \cup (C \cap A)[/tex].
Ilustrações
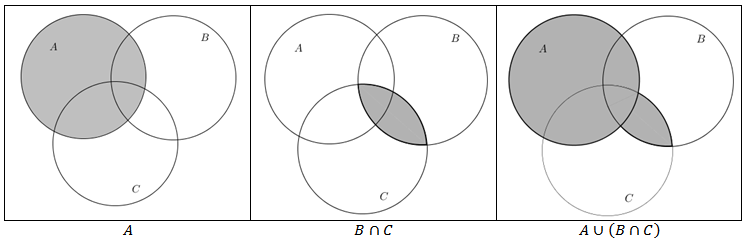
(1) Os próximos diagramas ilustram a propriedade distributiva [tex] A \cup (B \cap C) = (A \cup B) \cap (A \cup C)[/tex].
∎ Para obtermos a respectiva representação do conjunto [tex] A \cup (B \cap C)[/tex] seguimos os seguintes passos:
▪ Sombreamos o conjunto [tex]A[/tex];
▪ Sombreamos a interseção [tex]B \cap C[/tex];
▪ Sombreamos a união de [tex]A[/tex] e a interseção [tex]B \cap C[/tex].
∎ Para obtermos a respectiva representação do conjunto [tex] (A \cup B) \cap (A \cup C)[/tex] seguimos os seguintes passos:
▪ Sombreamos os conjuntos [tex]A[/tex] e [tex]B[/tex] para ilustrar a união [tex] A \cup B[/tex];
▪ Sombreamos os conjuntos [tex]A[/tex] e [tex]C[/tex] para ilustrar a união [tex] A \cup C[/tex];
▪ Fizemos a sobreposição das representações das uniões [tex]A \cup B \, [/tex] e [tex]A \cup C \, [/tex] e sombreamos a interseção.
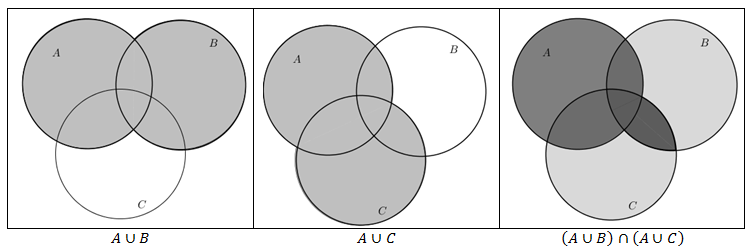
Observem que os sombreamentos finais dos dois passo a passos ilustram a igualdade em questão.
(2) Consideraremos [tex]A[/tex] e [tex]B[/tex] subconjuntos de um conjunto [tex]S[/tex]. Os próximos diagramas ilustram a primeira lei de De Morgan [tex]\overline{A} \cup \overline{B} = \overline{A \cap B}[/tex].
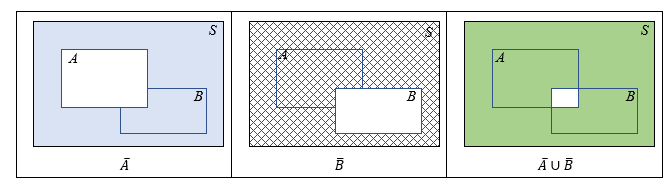
∎ Para a representação do conjunto [tex] \overline{A} \cup \overline{B}[/tex] seguimos os seguintes passos:
▪ Colorimos o complementar de [tex] A[/tex], com relação a [tex] S[/tex];
▪ Colorimos o complementar de [tex]B[/tex], com relação a [tex] S[/tex];
▪ Colorimos a união de [tex]\overline A[/tex] e [tex]\overline B[/tex].
∎ Para obtermos a representação do conjunto [tex]\overline{A \cap B}[/tex] seguimos os seguintes passos:
▪ Colorimos a interseção dos conjuntos [tex]A[/tex] e [tex]B[/tex];
▪ Colorimos o complementar da interseção [tex] A \cap B[/tex].
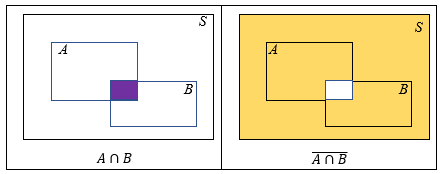
Observem que as regiões coloridas dos últimos diagramas dos dois passo a passos ilustram a igualdade em questão.
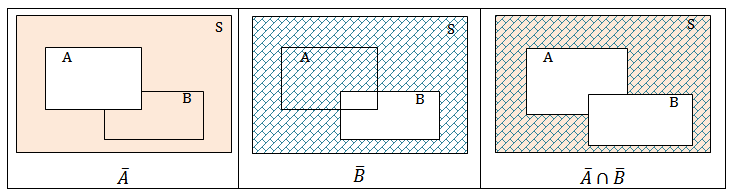
(3) Consideraremos [tex]A[/tex] e [tex]B[/tex] subconjuntos de um conjunto [tex]S[/tex]. Os próximos diagramas ilustram a segunda lei de De Morgan [tex]\overline{A} \cap \overline{B} = \overline{A \cup B}[/tex].
∎ Para a representação do conjunto [tex] \overline{A} \cap \overline{B}[/tex] seguimos os seguintes passos:
▪ Colorimos o complementar de [tex] A[/tex], com relação a [tex] S[/tex];
▪ Colorimos o complementar de [tex]B[/tex], com relação a [tex] S[/tex];
▪ Colorimos a interseção de [tex]\overline A[/tex] e [tex]\overline B[/tex].
∎ Para obtermos a representação do conjunto [tex]\overline{A \cup B}[/tex] seguimos os seguintes passos:
▪ Colorimos a união dos conjuntos [tex]A[/tex] e [tex]B[/tex];
▪ Colorimos o complementar da união [tex] A \cup B[/tex].
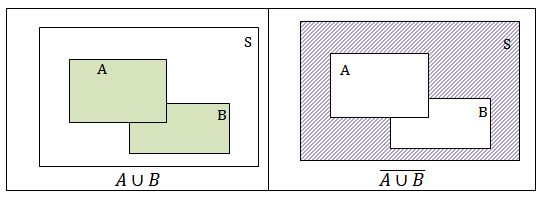
Observem que as regiões coloridas dos últimos diagramas dos dois passo a passos ilustram a igualdade em questão.
Para quem gosta de resolver exercícios …
V – Exercícios
1. Represente conjuntos pelos diagramas de Venn e ilustre as seguintes propriedades:
[tex]\qquad (A \cap \overline{B})\cup (A \cap B)=A[/tex]
[tex]\qquad (A \cap B) \cup (\overline{A} \cap B)= B[/tex]
[tex]\qquad (A \cap \overline{B})\cup (A \cap B) \cup (\overline{A} \cap B)=A \cup B[/tex]
2. Quais das seguintes igualdades são verdadeiras?
(a) [tex](A \cup B) \cap (A \cup C) = A \cup (B \cap C)[/tex]
(b) [tex]A \cup B = (A \cap \overline{B}) \cup B[/tex]
(c) [tex]\overline{A} \cap B = A \cup B[/tex]
(d) [tex](\overline{A \cup B}) \cap C = \overline{A} \cap \overline{B} \cap C[/tex]
(e) [tex](A \cap B) \cap (\overline{B} \cap C) = \emptyset[/tex]
(f) [tex](A \cap B) \cup (A \cap \overline{B}) = A[/tex]
 |
Observamos que os diagramas de Venn ilustram propriedades envolvendo conjuntos, mas não as demonstram. Demonstrações para esse tipo de propriedades exigem técnicas que não temos interesse em discutir nesta Sala. |
Equipe COM – OBMEP
