Problema
(Indicado a partir do 2º ano do E. M.)
Em um torneio de tiro, oito alvos são dispostos em três correntes penduradas, como mostra a figura abaixo.
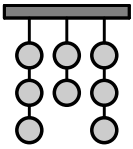
Os primeiros alvos de cada corrente estão presos a um suporte e os outros estão presos aos respectivos alvos imediatamente acima.
Para se ganhar a competição todos os oito alvos devem ser atingidos. Assim, se um competidor acertar um alvo sem ter atirado no(s) que está(ão) abaixo, este(s) cairá(ão) e o competidor não ganhará a pontuação relativa aos alvos perdidos.
Para obter a pontuação máxima do torneio, de quantas maneiras diferentes cada competidor pode acertar os oito alvos?
Solução
Vamos indicar por [tex]E[/tex], [tex]E[/tex] e [tex]E[/tex] os três alvos da esquerda, por [tex]M[/tex] e [tex]M[/tex] os dois alvos do meio e por [tex]D[/tex], [tex]D[/tex] e [tex]D[/tex] os três alvos da direita.
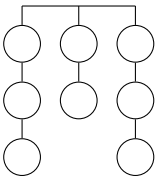
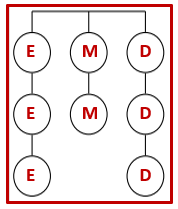
Se, por exemplo, considerarmos o anagrama [tex]EMDDMEED[/tex], podemos associá-lo à seguinte sequência de tiros:
-
1º tiro: O mais baixo da esquerda;
2º tiro: O mais baixo do meio;
3º tiro: O mais baixo da direita;
4º tiro: O segundo da direita;
5º tiro: O segundo do meio;
6º tiro: O segundo da esquerda;
7º tiro: O terceiro da esquerda e
8º tiro: O terceiro da direita.
Assim, para encontrarmos a quantidade de maneiras distintas que um competidor pode atirar, basta descobrir quantos anagramas a palavra [tex]EEEMMDDD[/tex] possui.
Portanto, cada competidor tem [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{8!}{3!2!3!}=560$} \, [/tex] maneiras diferentes de atirar e conseguir a pontuação máxima.
Solução elaborada pelos Moderadores do Blog.
 |
Se você gosta deste tipo de problema, visite esta Sala para encontrar outros problemas e aprender um pouco mais sobre essa técnica de resolução.
|
