Problemas Propostos

Problema 1 – Um grande jornal que circula no Ceará divulgou em 2012 o gráfico abaixo, referente aos casos de dengue, por bairro, em Fortaleza.

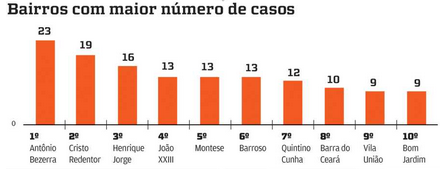
Qual a média, a moda e a mediana desse conjunto de dados?

Problema 2 – A média aritmética das idades de um grupo de 120 pessoas é de 40 anos. Se a média aritmética das idades das mulheres é de 35 anos e a dos homens é de 50 anos, qual o número de pessoas de cada sexo, no grupo?

Problema 3 – Para ser aprovado, um aluno precisa ter média maior ou igual a 5 . Se ele obteve notas 3 e 6 nas provas parciais (que têm peso 1 cada uma), quanto ele precisa tirar na prova final (que têm peso 2 ) para ser aprovado?

Problema 4 – Quatro amigos calcularam a média e a mediana de suas alturas, tendo encontrado como resultado 1.72m e 1.70m, respectivamente.
Qual a média entre a altura do mais alto e do mais baixo?

Problema 5 – Chama-se mediana de um conjunto de 50 dados ordenados em ordem crescente o número x dado pela média aritmética entre os 25º e o 26º dados. Observe no gráfico a seguir uma representação para as notas de 50 alunos do primeiro semestre de Ciências Econômicas numa determinada prova.

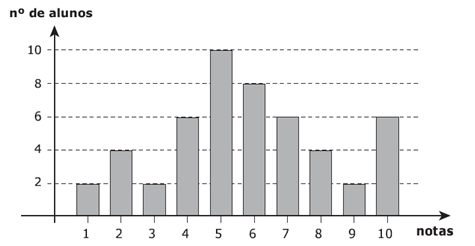
Determine a mediana das notas dos 50 alunos de Ciências Econômicas nesta prova.

Problema 6 – Numa pequena ilha, há cem pessoas que trabalham na única empresa ali existente. Seus salários (em moeda local) têm a seguinte distribuição de frequências:

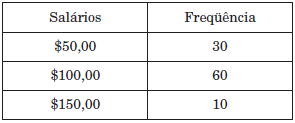
Qual a média dos salários das cem pessoas dessa empresa?

Problema 7 – Numa determinada prova, um conhecido professor observou que 50% dos seus alunos obtiveram nota exatamente igual a 4,0, 25% obtiveram média 6,4 e a média m do restante dos alunos foi suficiente para que a média geral ficasse em 5,9. Se quatro dos alunos que tiraram 4,0 e dois dos alunos do grupo cuja média foi m tivessem tirado 6,4, a média subiria para 6,0.
Determine o número de alunos da turma e o valor de m.

Problema 8 – Seis reservatórios cilíndricos, superiormente abertos e idênticos (A, B, C, D, E, F ) estão apoiados sobre uma superfície horizontal plana e ligados por válvulas (V) nas posições indicadas na figura.

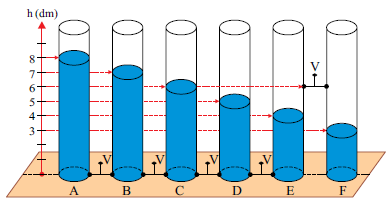
Com as válvulas (V) fechadas, cada reservatório contém água até o nível indicado. Todas as válvulas são, então, abertas, o que permite a passagem livre da água entre os reservatórios, até que se estabeleça o equilíbrio hidrostático.
Nesta situação final, o nível da água, em dm, será igual a
(a) 6,0 dm nos reservatórios de A a E e 3,0 dm no reservatório F.
(b) 5,5 dm nos reservatórios de A a E e 3,0 dm no reservatório F.
(c) 6,0 dm em todos os reservatórios.
(d) 5,5 dm em todos os reservatórios.
(e) 5,0 dm nos reservatórios de A a E e 3,0 dm no reservatório F.

Problema 9 – Uma Secretaria de Transportes investiga o número de passageiros que usam um serviço de trens e descobre que, em um dia em que há nove trens no total, o número de passageiros em cada um deles é de 32, 77, 111, 64, 28, 25, 116, 83, 47.
Assim, podemos concluir que:
(a) a mediana é de 64 passageiros, que é muito distante do valor da média, sugerindo que a distribuição dos dados é razoavelmente simétrica.
(b) a mediana é de 28 passageiros, que é muito distante do valor da média, sugerindo que a distribuição dos dados é razoavelmente simétrica.
(c) a mediana é de 64 passageiros, que é muito próxima do valor da média, sugerindo que a distribuição dos dados é razoavelmente simétrica.
(d) a mediana é de 28 passageiros, que é muito próxima do valor da média, sugerindo que a distribuição dos dados é razoavelmente simétrica.
(e) a mediana é de 77 passageiros, que é muito próxima do valor da média, sugerindo que a distribuição dos dados é razoavelmente simétrica.

Problema 10 – Uma escola utiliza um método de avaliação muito diferente dos tradicionais. O método consiste em:
I – Os alunos são submetidos a nove provas regulares de cada matéria ao longo do ano.
II – O aluno é considerado aprovado se a mediana das notas das nove provas for maior ou igual a sete.
III – Caso o aluno obtenha mediana das notas menor que sete, o mesmo é submetido a uma prova especial de recuperação na qual será aprovado se sua nota for maior ou igual a seis.
As seis primeiras notas do aluno Benedito foram 7, 8, 3, 5, 9, 5. Sabendo que a mediana das notas de Benedito foi a maior possível, então,
(a) Benedito foi reprovado, pois sua mediana foi igual a 4.
(b) Benedito foi reprovado, pois sua mediana foi igual a 6.
(c) Benedito foi aprovado, pois sua mediana foi igual a 6,2.
(d) Benedito foi aprovado, pois sua mediana foi igual a 7.
(e) Benedito foi aprovado, pois sua mediana foi igual a 8.

Problema 11 – Em um treinamento de salto em altura para escolha do representante de um país numa competição internacional, os atletas A, B e C realizaram quatro saltos cada um. Abaixo seguem as marcas obtidas pelos mesmos

• Atleta A: 148 cm, 170 cm, 155 cm e 131 cm;
• Atleta B: 145 cm, 151 cm, 150 cm e 152 cm;
• Atleta C: 146 cm, 151 cm, 143 cm e 160 cm;

Para essa competição, o técnico escolhe o representante do país pelo desempenho em relação à média dos saltos. Sabendo que na edição anterior dessa mesma competição o atleta C foi o representante desse país, então para essa competição
(a) o atleta C deve continuar representando o país, pois o mesmo apresenta melhor média nos saltos.
(b) o atleta B deve representar o país no lugar do atleta C , uma vez que sua média nos saltos é melhor.
(c) os atletas B ou C podem representar o país, uma vez que suas médias são iguais.
(d) os atletas A ou B podem representar o país, uma vez que suas médias são iguais.
(e) o atleta A deve representar o país, pois é dele a melhor média nos saltos.

Problema 12 – Numa classe com vinte alunos as notas do exame final podiam variar de 0 a 100 e a nota mínima para aprovação era 70. Realizado o exame, verificou-se que oito alunos foram reprovados. A média aritmética das notas desses oito alunos foi 65, enquanto que a média dos aprovados foi 77. Após a divulgação dos resultados, o professor verificou que uma questão havia sido mal formulada e decidiu atribuir 5 pontos a mais para todos os alunos. Com essa decisão, a média dos aprovados passou a ser 80 e a dos reprovados 68,8.
(a) Calcule a média aritmética das notas da classe toda antes da atribuição dos cinco pontos extras.
(b) Com a atribuição dos cinco pontos extras, quantos alunos, inicialmente reprovados, atingiram nota para aprovação?

Problema 13 – Num concurso vestibular para dois cursos, A e B, compareceram 500 candidatos para o curso A e 100 candidatos para o curso B. Na prova de matemática, a média aritmética geral, considerando os dois cursos, foi 4. Mas considerando-se apenas os candidatos ao curso A, a média cai para 3,8. Qual a média dos candidatos ao curso B na prova de matemática?