Segredo 8

Viajando pelo Triângulo de Pascal
Segredos do Triângulo de Pascal

Segredo 8

A Sequência de Fibonacci é uma sequência de números naturais na qual os dois primeiros termos são iguais a 1 e, a partir do terceiro, cada termo é definido pela soma dos dois termos imediatamente anteriores a ele.
Assim, os primeiros termos dessa sequência são 1, 1, 2, 3, 5, 8, 13, 21, … .
Já encontramos a chamada Sequência de Fibonacci em alguns problemas do nosso Blog. Será que vocês conseguem encontrá-la no Triângulo de Pascal?

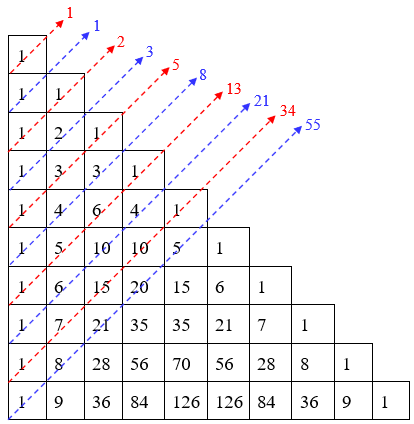
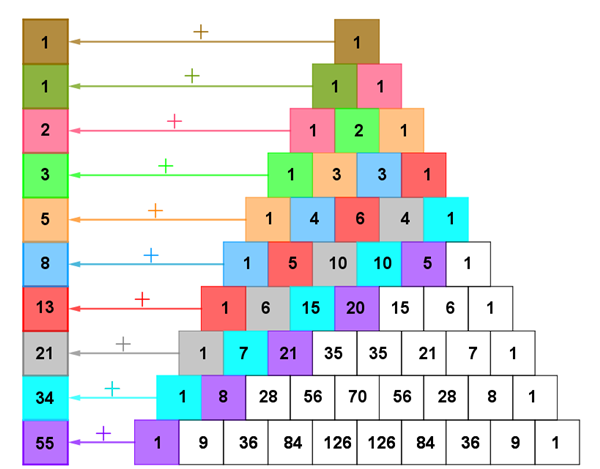
Segredo 8: A partir da representação do Triângulo de Pascal como um triângulo retângulo, trace paralelas sucessivas conforme abaixo indicado. As somas dos números dispostos ao longo dessas paralelas geram a sucessão de Fibonacci:
[tex]\textcolor{#68a597}{\left(1,1,2,3,5,8,13,21,34,\dots\right)}[/tex].

A visualização da Sequência de Fibonacci fica mais natural quando utilizamos o Triângulo de Pascal representado por um triângulo retângulo; no entanto, podemos também utilizar a representação na forma de um triângulo isósceles.

E, aproveitando a oportunidade, assista a um vídeo sobre a Sequência de Fibonacci.

Um vídeo para relaxar aprendendo. . .

Para assistir, cliquem na setinha.

Equipe COM – OBMEP

Voltar para Sala Inicial de Segredos