Segredos do Triângulo de Pascal
Segredo 16
Vocês conhecem esta questão do ENEM?
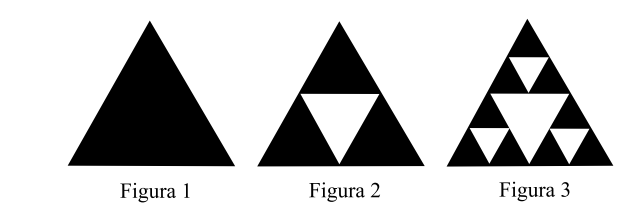
O triângulo de Sierpinski, uma das formas elementares da geometria fractal, pode ser obtido por meio dos seguintes passos:
1. comece com um triângulo equilátero (figura 1);
2. construa um triângulo em que cada lado tenha a metade do tamanho do lado do triângulo anterior e faça três cópias;
3. posicione essas cópias de maneira que cada triângulo tenha um vértice comum com um dos vértices de cada um dos outros dois triângulos, conforme ilustra a figura 2;
4. repita sucessivamente os passos 2 e 3 para cada cópia dos triângulos obtidos no passo 3 (figura 3).
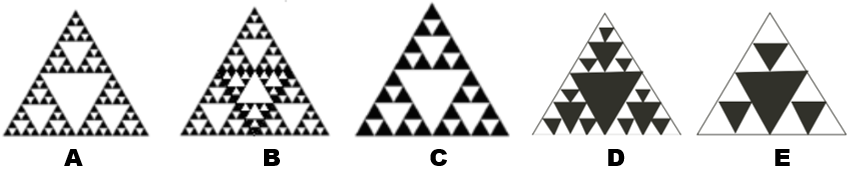
De acordo com o procedimento descrito, a figura 4 da sequência apresentada acima é
O vídeo a seguir pode ajudar com a resposta da questão.
Conhecendo ou não a questão, vocês devem estar se perguntando: Cadê o Triângulo de Pascal?
Então, vamos lá!
Para este segredo, vamos utilizar a representação do Triângulo de Pascal como um triângulo isósceles e vamos colorir de maneira conveniente as entradas: as entradas contendo números ímpares serão pintadas com fundo preto e as entradas contendo números pares serão pintadas com fundo branco.
Imagem extraída de Cuaderno de Cultura Científica
Observe que a figura obtida segue o mesmo padrão do Triângulo de Sierpinski que, conforme vimos na questão do ENEM, é um tipo de fractal – uma figura geométrica com padrão de repetição infinito.
Para efeito de comparação, na imagem a seguir usamos um Triângulo de Pascal com menos linhas que o da imagem anterior.
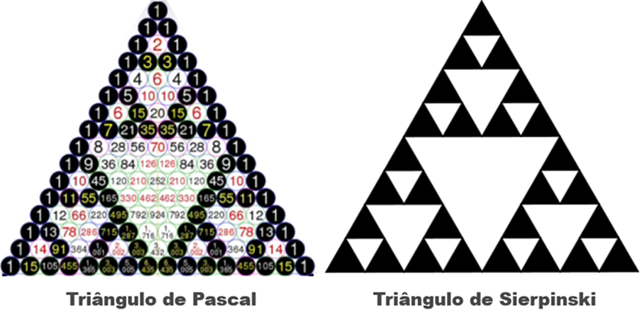
Segredo 16: Se na representação do Triângulo de Pascal como um triângulo isósceles colorirmos as entradas contendo números ímpares com uma cor e as entradas contendo números pares com outra, o resultado será um triângulo com o mesmo padrão do Triângulo de Sierpinski.
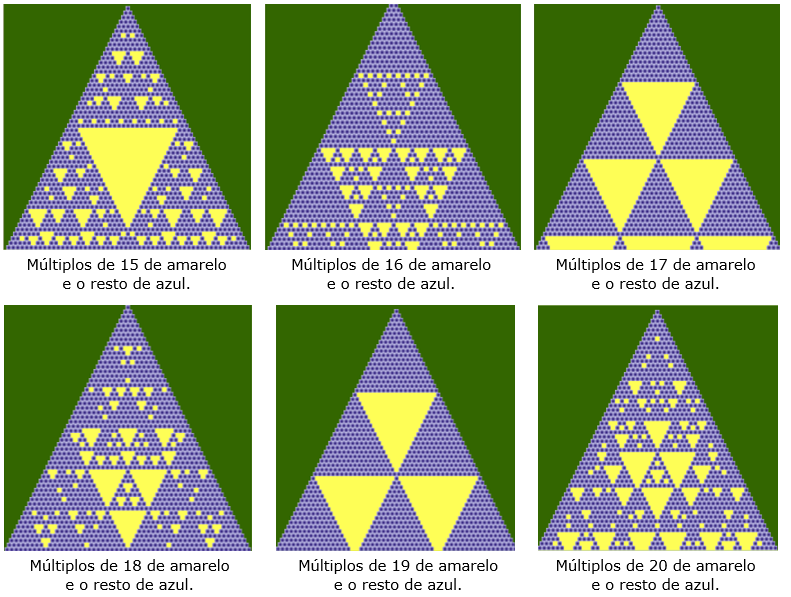
Se vocês se interessaram por essas imagens geradas pelo Triângulo de Pascal, vejam outras também obtidas ao colorir as entradas de azul e amarelo, mas usando outros critérios para colorir. É só clicar no botão abaixo.
Equipe COM – OBMEP