Segredo 14

Lembrem-se de que estamos interessados nos “caminhos mais curtos” e podemos nos mover apenas “da esquerda para a direita” ou “de cima para baixo”, sem voltarmos.
Vejamos alguns exemplos.

• Observem que só existe um caminho curto do ponto A até qualquer ponto do lado superior ou do lado esquerdo da malha.
  
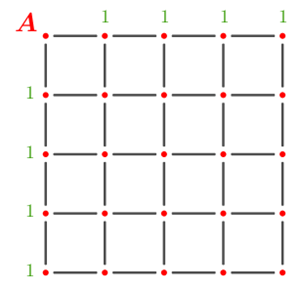
• De A até o ponto que está na segunda linha da segunda coluna, existem dois caminhos curtos.
  
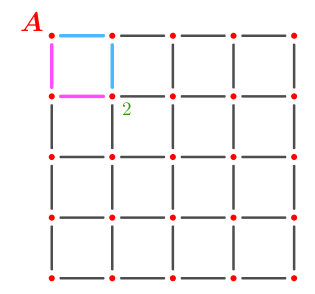
• De A até o ponto que está na segunda linha da terceira coluna, existem três caminhos curtos.
  
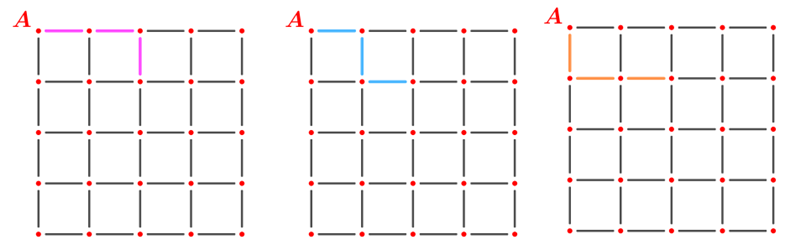
• De maneira simétrica, existem três caminhos curtos de A até o ponto que está na terceira linha da segunda coluna.
  
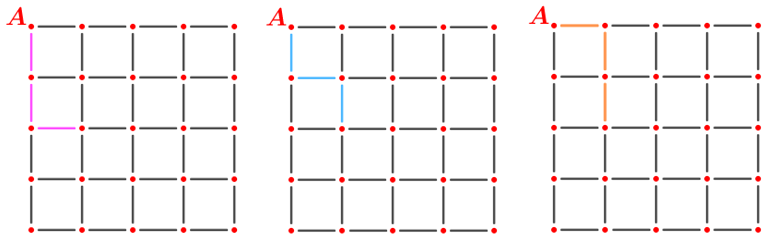
• Agora, de A até o ponto que está na segunda linha da quarta coluna, existem quatro caminhos curtos.
  
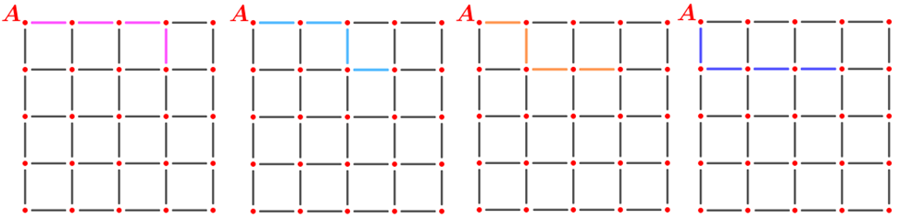
• De maneira simétrica, existem quatro caminhos curtos de A até o ponto que está na quarta linha da segunda coluna.
  

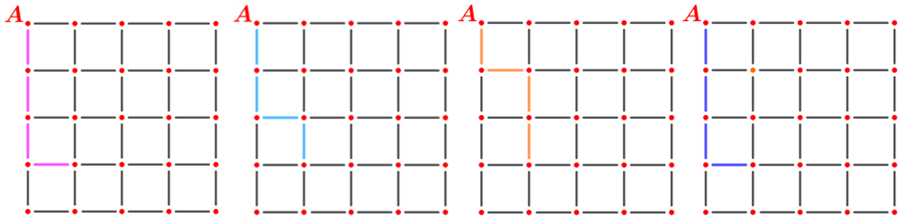
Vamos reunir esses resultados em uma só figura!

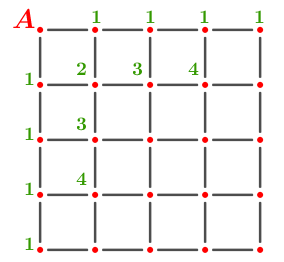
Mais uma ajudinha?
Olha ele aí!!!!!!!!

---

---

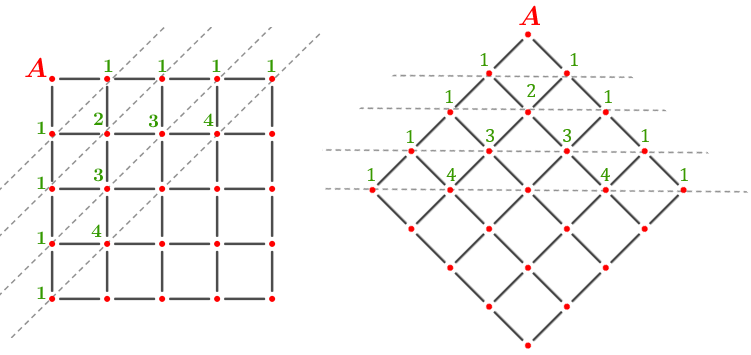
Podemos interpretar a malha quadriculada como os quarteirões de uma cidade e explorar a chamada “Geometria do Taxista”, na qual os quarteirões são respeitados para irmos de um ponto a outro.
Nesse tipo de geometria, a menor distância entre dois pontos nem sempre é a medida do segmento de reta que os une (como na geometria euclidiana), já que, como em uma cidade, não é possível atravessar as casas dos quarteirões para sair de um ponto e chegar em outro.
Como no jogo, o caminho mais curto é um percurso entre duas localidades que tenha o número mínimo de quarteirões.

---

---

Segredo 14: A bela relação entre o Triângulo de Pascal e a Geometria do Taxista.

---

---

Equipe COM – OBMEP