Segredo 10

Deu certo?
Vejam só:

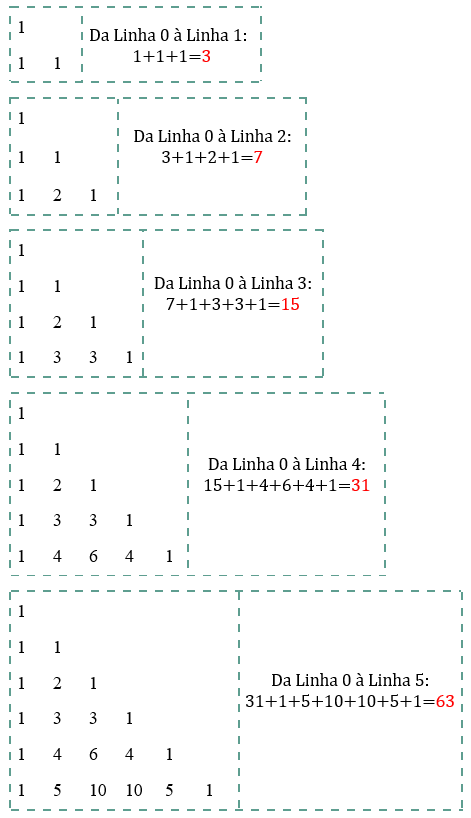
Vamos conferir mais algumas somas!

• Da Linha 0 à Linha 6:
  [tex]63+1+6+15+20+15+6+1=\textcolor{red}{127}[/tex];
• Da Linha 0 à Linha 7:
  [tex]127+1+7+21+35+35+21+7+1=\textcolor{red}{255}[/tex];
• Da Linha 0 à Linha 8:
  [tex]255+1+8+28+56+70+56+28+8+1=\textcolor{red}{511}[/tex].

Bom, se vocês estão pensando que números são esses, aqui vai a resposta:

• [tex]3,\,7,\,15,\,31,\,63,\,127, \,255, \,511[/tex] são os oito primeiros Números de Mersenne.

Os Números de Mersenne são números naturais da forma:
[tex]\qquad \qquad M_n = 2^n – 1[/tex].
Particularmente, se
[tex]\qquad \qquad M_n[/tex] for um número primo,
ele será dito um primo de Mersenne.
Em janeiro de 2019 foi descoberto o maior primo de Mersenne, até o momento.
Ele é o 51º primo de Mersenne e corresponde a n = 82 589 933:
[tex]~~\\
\qquad \qquad M_{82589933} = 2^{82589933}-1\,.\\
[/tex]
Esse primo tem, simplesmente, 24 862 048 dígitos!

Segredo 10: Ao somarmos todas as entradas de um Triângulo de Pascal de [tex]n[/tex] linhas, obtemos o enésimo número de Mersenne: [tex] \textcolor{#68a597}{M_n = 2^n – 1}[/tex]. (Particularmente, [tex] \textcolor{#68a597}{M_0 = 0}[/tex] e [tex] \textcolor{#68a597}{M_1 = 1}[/tex].)

Equipe COM – OBMEP