Um pouco sobre congruência de triângulos
Uma estoriazinha para começar…
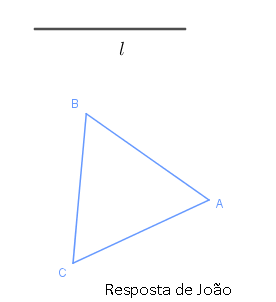
- A professora de José e de João deixou como tarefa a construção de um triângulo, a partir das seguintes instruções:
- Construa um triângulo equilátero [tex]ABC[/tex] de lados com comprimento [tex]l[/tex].
[tex]\qquad \qquad \stackrel{\underline{\qquad \qquad \quad \quad \qquad }}{l}[/tex]
No dia seguinte, recebeu as respostas de José e de João e, muito feliz, comprovou que ambas estavam corretas!
|
|
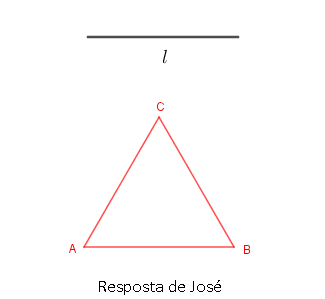 |
- Utilize o applet abaixo e comprove que, de fato, as respostas dos dois alunos estavam corretas.
Instruções:
1) Aguarde o aplicativo carregar completamente.
2) Para transladar os triângulos ou o segmento, clique sobre os pontos [tex]T_1[/tex], [tex]T_2[/tex] ou [tex]T_3[/tex] e, mantendo o mouse pressionado, movimente o respectivo objeto horizontal ou verticalmente.
3) Para rodar os triângulos ou o segmento, clique sobre os pontos [tex]R_1[/tex], [tex]R_2[/tex] ou [tex]R_3[/tex] e, mantendo o mouse pressionado, rode o respectivo objeto.
4) Utilize as setinhas que aparecem no canto superior direito do aplicativo, para voltar à configuração inicial.
- Afinal, os triângulos desenhados por José e por João são iguais?
O que são triângulos congruentes?
A estoriazinha acima mostra a necessidade de se precisar o que significa dois triângulos serem iguais. Intuitivamente, dois triângulos distintos são iguais se for possível mover um deles, sem deformá-lo, até fazê-lo coincidir com o outro. Matematicamente dois triângulos com essa característica são ditos congruentes e essa "igualdade" entre triângulos recebe o nome de congruência .
Vamos precisar o que são triângulos congruentes.
Dois triângulos são ditos congruentes se existir uma correspondência entre os vértices de um e os do outro, de modo que
(i) ângulos internos correspondentes são congruentes (têm a mesma medida);
(ii) lados correspondentes são congruentes (têm a mesma medida).
Na figura abaixo, os triângulos [tex]ABC[/tex] e [tex]DEF[/tex] com a seguinte correspondência entre vértices:
[tex]A\longleftrightarrow D\qquad \qquad [/tex] [tex]B\longleftrightarrow E\qquad \qquad[/tex] [tex]C\longleftrightarrow F[/tex]
são congruentes.
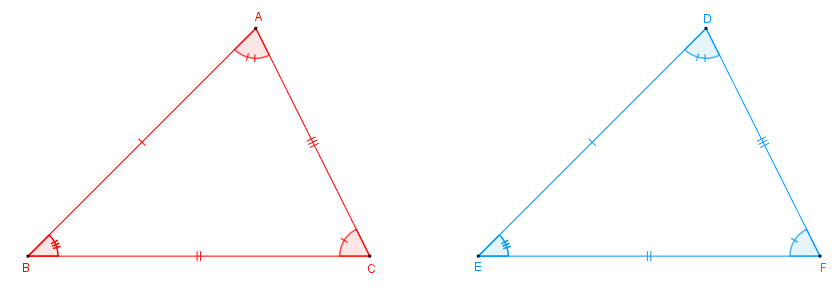
Para indicarmos que a correspondência [tex]ABC \longleftrightarrow DEF[/tex] é uma congruência e, consequentemente, os triângulos [tex]ABC[/tex] e [tex]DEF[/tex] são congruentes, escrevemos [tex]\triangle ABC \cong \triangle DEF.[/tex]
Essa notação é muito eficiente, pois a expressão [tex]\triangle ABC \cong \triangle DEF[/tex] nos dá seis informações:
● Os ângulos [tex]\widehat{A}[/tex] e [tex]\widehat{D}[/tex] têm a mesma medida.
● Os ângulos [tex]\widehat{B}[/tex] e [tex]\widehat{E}[/tex] têm a mesma medida.
● Os ângulos [tex]\widehat{C}[/tex] e [tex]\widehat{F}[/tex] têm a mesma medida.
● Os lados [tex]\overline{AB}[/tex] e [tex]\overline{DE}[/tex] têm o mesmo comprimento. ([tex]AB=DE[/tex])
● Os lados [tex]\overline{BC}[/tex] e [tex]\overline{EF}[/tex] têm o mesmo comprimento. ([tex]BC=EF[/tex])
● Os lados [tex]\overline{CA}[/tex] e [tex]\overline{FD}[/tex] têm o mesmo comprimento. ([tex]CA=FD[/tex])
Observem quantas informações importantes no estudo da geometria vocês conseguem obter sabendo que dois dados triângulos são congruentes. São três igualdades de medidas de ângulos e três igualdades de comprimentos de segmentos.
Se dependêssemos apenas da definição de congruência seria necessário termos em mãos doze medidas para verificarmos se dois dados triângulos são congruentes:
– as medidas dos três ângulos internos do primeiro triângulo;
– as medidas dos três lados do primeiro triângulo;
– as medidas dos três ângulos internos do segundo triângulo;
– as medidas dos três lados do segundo triângulo.
No entanto, existem propriedades com as quais é possível concluir que dois triângulos são congruentes, a partir de um número menor de medidas conhecidas do que as doze que a definição exige. Essas propriedades são conhecidas como casos (ou critérios) de congruência.
Casos de congruência de triângulos
As propriedades enunciadas a seguir apresentam condições mínimas que, se verificadas, nos permitem afirmar que dois triângulos são congruentes.
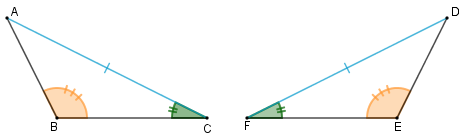
Se dois triângulos têm ordenadamente congruentes dois ângulos e o lado compreendido por eles, então estes triângulos são congruentes.
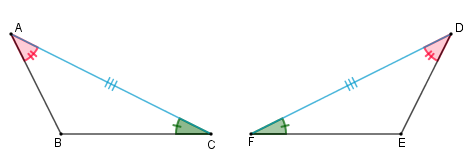
Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes.
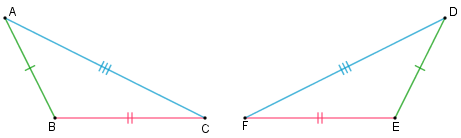
Se dois triângulos têm ordenadamente congruentes os três lados, então estes triângulos são congruentes.
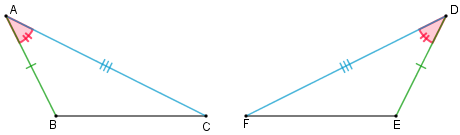
Se dois triângulos têm ordenadamente congruentes um lado, um ângulo adjacente e o ângulo oposto a esse lado, então estes triângulos são congruentes.
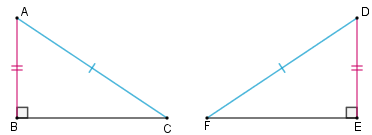
Se dois triângulos retângulos têm ordenadamente congruentes um cateto e a hipotenusa, então estes triângulos são congruentes.
Uma aplicação especial do caso L.A.L.
Os ângulos da base de um triângulo isósceles são congruentes (têm a mesma medida).
Justificativa:
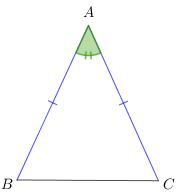
Seja [tex]ABC[/tex] um triângulo isósceles, tal que os segmentos [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex] têm a mesma medida.
Vamos comparar o triângulo [tex]ABC[/tex] com ele mesmo, considerando a correspondência [tex]ABC\longleftrightarrow ACB[/tex], isto é,
[tex]B\longleftrightarrow C\qquad \qquad[/tex] [tex]A\longleftrightarrow A\qquad \qquad[/tex] [tex]C\longleftrightarrow B.[/tex]
Perceba que:
- os segmentos [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex] têm o mesmo comprimento;
- os ângulos [tex]B\hat{A}C[/tex] e [tex]C\hat{A}B[/tex] têm a mesma medida;
- os segmentos [tex]\overline{AC}[/tex] e [tex]\overline{AB}[/tex] têm o mesmo comprimento;
assim, pelo caso L.A.L, temos que [tex]\triangle ABC \cong \triangle ACB[/tex] e com isso, particularmente, os ângulos [tex]A\hat{B}C[/tex] e [tex]A\hat{C}B[/tex] têm a mesma medida.
 |
Esperamos que você tire proveito da apresentação feita aqui. |
Equipe COM – OBMEP
Dezembro de 2017.