.Sala para leitura_030: Ângulo Central e Ângulo Inscrito

Ângulo Central e Ângulo Inscrito

Vamos discutir a relação entre as medidas de dois ângulos importantes que podemos definir a partir de uma circunferência.
Mas, antes, vamos recordar algumas nomenclaturas…
Bom proveito!

Definições iniciais

Ângulo é a união de duas semirretas com a mesma origem.
Fixado um ângulo, as semirretas que o definem são chamadas de lados desse ângulo e a origem comum é o vértice do ângulo em questão.

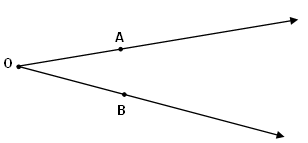
Na figura ao lado, podemos observar o ângulo definido pelas semirretas [tex]\stackrel{\longrightarrow}{OA}[/tex] e [tex]\stackrel{\longrightarrow}{OB}[/tex]. Esse é o chamado ângulo [tex]AOB[/tex] e pode ser denotado por:

[tex]A\hat{O}B[/tex], [tex]B\hat{O}A[/tex], [tex]\angle AOB[/tex], [tex]\angle BOA[/tex] ou, simplesmente, [tex]\hat{O}[/tex].

Assim:

o ângulo [tex]A\hat{O}B[/tex] é a reunião das semirretas [tex]\stackrel{\longrightarrow}{OA}[/tex] e [tex]\stackrel{\longrightarrow}{OB}[/tex], ou seja, o conjunto formado por todos os pontos das duas semirretas;
o ponto [tex]O[/tex] é o vértice do ângulo [tex]A\hat{O}B[/tex];
[tex]\stackrel{\longrightarrow}{OA}[/tex] e [tex]\stackrel{\longrightarrow}{OB}[/tex] são os lados do ângulo [tex]A\hat{O}B[/tex].

Uma semirreta pode ser definida a partir de um segmento de reta; assim é comum não colocarmos nas representações geométricas de um ângulo as setinhas que indicariam as semirretas que definem os seus lados.

Chamamos ângulo central de uma dada circunferência a qualquer ângulo que tenha vértice no centro dessa circunferência.

Exemplos de ângulos centrais da circunferência [tex]\lambda[/tex]:

[tex]A \hat{O}B[/tex]: ângulo definido pelas semirretas [tex]\stackrel{\longrightarrow}{OA}[/tex] e [tex]\stackrel{\longrightarrow}{OB}[/tex];
[tex]B \hat{O}C[/tex]: ângulo definido pelas semirretas [tex]\stackrel{\longrightarrow}{OB}[/tex] e [tex]\stackrel{\longrightarrow}{OC}[/tex];
[tex]D \hat{O}C[/tex]: ângulo definido pelas semirretas [tex]\stackrel{\longrightarrow}{OD}[/tex] e [tex]\stackrel{\longrightarrow}{OC}[/tex];
[tex]B \hat{O}D[/tex]: ângulo definido pelas semirretas [tex]\stackrel{\longrightarrow}{OB}[/tex] e [tex]\stackrel{\longrightarrow}{OD}[/tex];
[tex]A \hat{O}C[/tex]: ângulo definido pelas semirretas [tex]\stackrel{\longrightarrow}{OA}[/tex] e [tex]\stackrel{\longrightarrow}{OC}[/tex];

Como os lados de um ângulo são semirretas, necessariamente os lados de um ângulo central intersectam a circunferência que o define. Assim, todo ângulo central [tex]A \hat{O}B[/tex] determina um arco [tex]\stackrel{\frown}{AB}[/tex] na circunferência onde ele está definido.
Reciprocamente, a todo arco [tex]\stackrel{\frown}{AB}[/tex] definido em uma circunferência de centro [tex]O[/tex] corresponde um ângulo central [tex]A \hat{O}B[/tex].
O arco [tex]\stackrel{\frown}{AB}[/tex] (ou [tex]\stackrel{\frown}{BA}[/tex]) é, então, dito:

o arco correspondente ao ângulo central [tex]\hat{O}[/tex],
ou o arco subentendido por [tex]\hat{O}[/tex],
ou, ainda, o arco visto ou enxergado pelo ângulo [tex]\hat{O}[/tex].

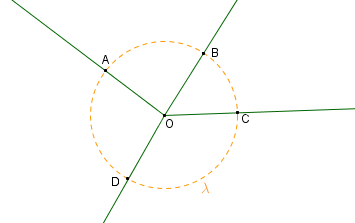Em termos de medidas, a medida angular em graus de um arco de uma circunferência é a medida em graus do ângulo central correspondente.

Ângulo inscrito relativo a uma dada circunferência é qualquer ângulo que tenha o vértice nessa circunferência e os lados secantes a ela.

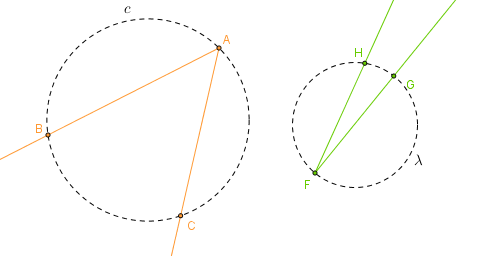
Na figura ao lado,

sendo [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] pontos da circunferência [tex]c[/tex], [tex]B \hat{A}C[/tex] é um ângulo inscrito na circunferência [tex]c[/tex];
sendo [tex]F[/tex], [tex]G[/tex] e [tex]H[/tex] pontos da circunferência [tex]\lambda[/tex], [tex]G \hat{F}H[/tex] é um ângulo inscrito na circunferência [tex]\lambda[/tex].

Aqui também podemos dizer que [tex]\stackrel{\frown}{BC}[/tex], ou [tex]\stackrel{\frown}{CB}[/tex], é o arco visto ou enxergado pelo ângulo [tex] \hat{A}[/tex] e que [tex]\stackrel{\frown}{HG}[/tex], ou [tex]\stackrel{\frown}{GH}[/tex], é o arco visto ou enxergado pelo ângulo [tex]\hat{F}[/tex].

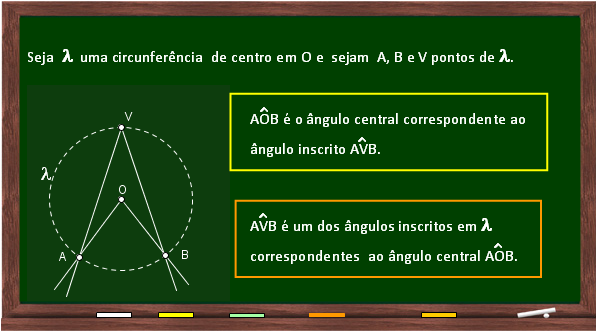
Três resultados importantes

As medidas desses dois ângulos estão relacionadas.
Você conhece essa relação?

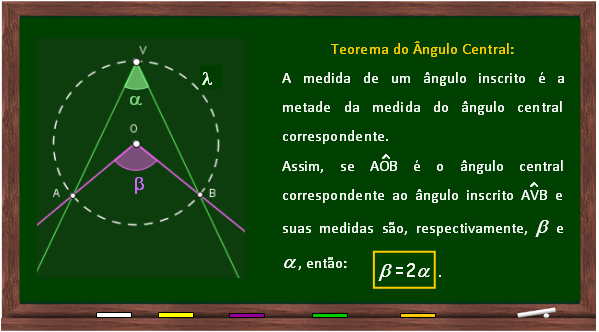
(Se você quiser saber como podemos estabelecer essa relação, visite esta Sala.)

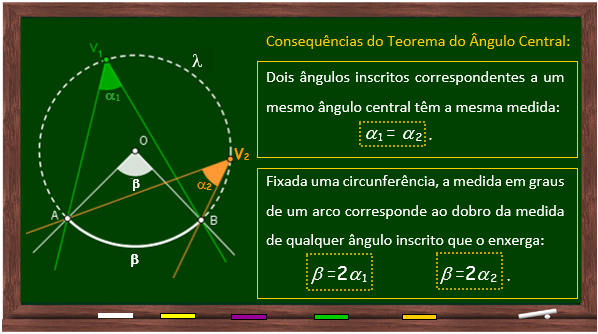
Estes são dois resultados importantes envolvendo ângulos inscritos e que são consequência do Teorema do ângulo central e das definições aqui apresentadas.

Equipe COM – OBMEP

Fevereiro de 2018.