O Buraco do Triângulo
 |
Você conhece este problema? |
Ao tentarmos formar a mesma figura com outra disposição dos mesmos polígonos, surge um buraco.
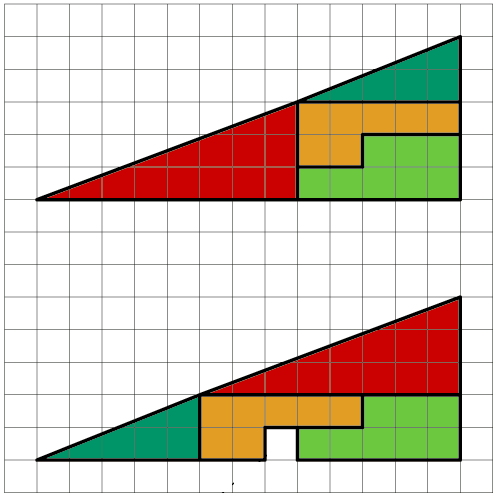 Onde está o erro? Como o buraco surgiu?
Onde está o erro? Como o buraco surgiu?

 |
Antes de ler a solução, utilize o applet abaixo para tentar descobrir por que apareceu o buraco… |
 |
Observamos que o applet ajuda na visualização do resultado; mas, matematicamente, não substitui sua demonstração. |
Desvendando o mistério…
A figura é uma forma de “ilusão de ótica” e nos engana.
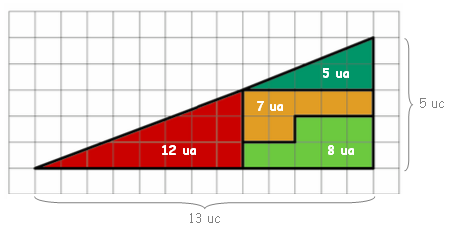
Observe que, em um primeiro momento, pensamos que a primeira disposição dos polígonos internos define um grande triângulo retângulo com catetos medindo [tex]5[/tex] e [tex]13[/tex] unidades de comprimento. Mas, depois de alertados de que "algo estranho" aconteceu, observamos que isso não é verdade: a soma total das áreas dos quatro polígonos é [tex]\boxed{12+8+7+5=32}[/tex] unidades de área enquanto o suposto triângulo que as envolve, sem sobrar ou faltar pedaço, tem [tex]\boxed{\dfrac{13 \times 5}{2}=32,5}[/tex] unidades de área.
Mais ainda, não é possível alinharmos as hipotenusas dos triângulos vermelho e verde. Isso mesmo, em cada figura, os pontos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] não estão alinhados!
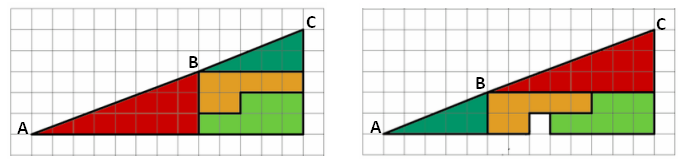
Com efeito, os catetos horizontais dos triângulos verde e vermelho estão na razão [tex]\dfrac{5}{8}[/tex], enquanto os verticais estão na razão [tex]\dfrac{2}{3}[/tex]. Como [tex]\dfrac{2}{3}\not=\dfrac{5}{8}[/tex], esses dois triângulos não são semelhantes e, então, particularmente os ângulos [tex]\alpha[/tex] e [tex]\beta[/tex] não são congruentes, ou seja, as inclinações das hipotenusas dos triângulos verde e vermelho são diferentes. (Para mais informações sobre semelhança de triângulos, consulte esta sala.)
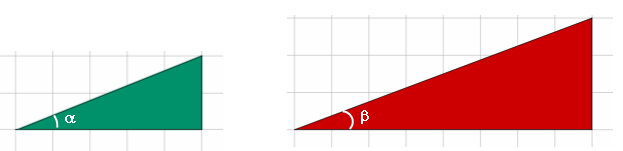
Para quem já aprendeu trigonometria, é fácil calcular a medida dos ângulos [tex]\alpha[/tex] e [tex]\beta[/tex]:
[tex]\qquad \qquad \boxed{\alpha\approx 21,8^{\circ}}\quad[/tex] e [tex]\quad \boxed{\beta\approx 20,6^{\circ}}[/tex].
Essa diferença de inclinação pode ser percebida visualmente com o applet: basta colocar um triângulo sobre o outro, de modo a coincidir os respectivos vértices dos ângulos [tex]\alpha[/tex] e [tex]\beta[/tex].
Essas contas mostram que, de fato, fomos enganados. A dita "hipotenusa" determinada pelos pontos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] sequer é um segmento de reta…
- Perceba que ao fazermos a primeira montagem com o applet, surge uma faixa branca entre a hipotenusa do triângulo externo e as hipotenusas não alinhadas dos triângulos vermelho e verde. É parte da área dessa faixa que fica concentrada e determina o aparecimento do quadrado, quando fazemos a segunda montagem.
- Note, também, que a diferença entre as áreas das quatro peças utilizadas e do suposto triângulo que as envolveria é
[tex]\boxed{ 0,5}[/tex] unidades de área, uma área menor do que a do quadrado que apareceu na segunda montagem.
Isso se deve ao fato de que, nessa montagem, parte das áreas dos triângulos coloridos define uma faixa externa ao triângulo [tex]5 \times 13[/tex].

Um vídeo para terminar
Assista ao vídeo e veja que o matemático Rogério Martins também andou à procura do Buraco do Triângulo…
Para assistir, é só clicar na setinha.
Equipe COM – OBMEP
Setembro de 2017.
