Para aqueles que sabem o que é uma Progressão Aritmética – PA , basta observar que a fórmula da soma dos [tex]n[/tex] primeiros termos da PA [tex](a_1, \, a_2, \, a_3, \, \ldots \, , \, a_n, \, \ldots)[/tex] é dada por
[tex]\qquad \qquad S_n=a_1+a_2+\ldots+a_n=\dfrac{(a_1+a_n)\cdot n}{2}[/tex].
Como [tex](1, \, 2, \, 3, \, 4, \, \ldots \, , \, t, \, t+1, \, \ldots)[/tex] é uma PA, de razão [tex]1[/tex], segue que a soma dos [tex]t[/tex] primeiros termos é dada por:
[tex]\qquad \qquad \boxed{1+2+3+ \cdots+t=\dfrac{(1+t)\cdot t}{2}}[/tex].
Assim, particularmente:
✓ [tex]1+2+3+ \cdots+10=\dfrac{(1+10)\cdot 10}{2}=\dfrac{11\cdot 10}{2}=11\cdot 5=55[/tex];
✓ [tex]1+2+3+ \cdots+100=\dfrac{(1+100)\cdot 100}{2}=\dfrac{101\cdot 100}{2}=101\cdot 50=5050[/tex];
✓ [tex]1+2+3+ \cdots+1000=\dfrac{(1+1000)\cdot 1000}{2}=\dfrac{1001\cdot 1000}{2}=1001\cdot 500=500500[/tex];
✓ [tex]1+2+3+ \cdots+5000=\dfrac{(1+5000)\cdot 5000}{2}=\dfrac{5001\cdot 5000}{2}=5001\cdot 2500=12502500[/tex].
Que fórmula fantástica, não é?
Com ela obtemos com a mesma facilidade uma soma com dez, com mil ou com cinco mil parcelas!
Mas, embora útil, alguém que não saiba o que é uma PA poderá ficar na dúvida se essa fórmula funciona sempre. Assim, vamos mostrar como obtê-la por dois caminhos diferentes e sem utilizar progressões aritméticas. Em cada caminho, vamos simplesmente fazer continhas agrupando de forma conveniente as parcelas da soma [tex]1+2+3+ \cdots+t[/tex].
Vejamos.
Método I
Se [tex]t[/tex] é um número natural maior do que [tex]1[/tex], observe inicialmente que
[tex]\qquad \qquad 1+2+\cdots+(t-1)+t=t+(t-1)+\cdots+2+1[/tex],
portanto:
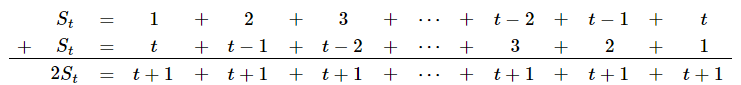
Assim, [tex]2S_t=t\cdot (t+1)[/tex] e podemos concluir que:
[tex]\qquad \qquad \boxed{S_t=\dfrac{t\cdot (t+1)}{2}}[/tex].
Para você entender direitinho o que aconteceu com as parcelas centrais de [tex] S_t[/tex], quando somamos as duas igualdades, vamos refazer a soma considerando dois casos: [tex]t[/tex] par e [tex]t[/tex] ímpar.
✓ Para [tex]t[/tex] par, observe que:
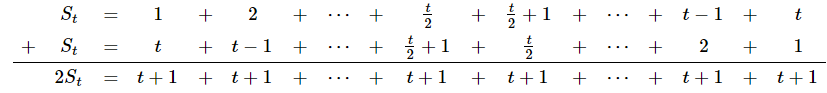
Com isso, [tex]2S_t=t\cdot(t+1)[/tex] e podemos assim concluir que [tex]S_t=\dfrac{t\cdot(t+1)}{2}[/tex].
✓ Para [tex]t[/tex] ímpar, observe que:
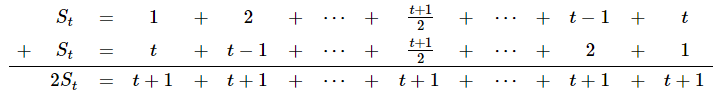
Aqui também, [tex]2S_t=t\cdot(t+1)[/tex] e [tex] S_t=\dfrac{t\cdot(t+1)}{2}[/tex].
Método II
Seja [tex]t[/tex] um número natural maior do que [tex]1.[/tex]
✓ Suponha que [tex]t[/tex] seja par; assim podemos agrupar os [tex]t[/tex] números [tex]1, \, 2, \, 3, \, 4, \, \ldots \, , \, t[/tex] de dois em dois, conforme mostra a figura abaixo, e somá-los.

[tex] \quad\begin{align*} &1+2+3 \cdots+t= {\color{red}{1}}+{\color{#1E90FF}{2}}+{\color{#FF8C00}{3}}+{\color{#32CD32}{4}}+ \cdots+{\color{#32CD32}{(t-3)}}+{\color{#FF8C00}{(t-2)}}+{\color{#1E90FF}{(t-1)}}+{\color{red}{t}}=\\
&=\underbrace{{\color{red}{[1+t]}}+{\color{#1E90FF}{[2+(t-1)]}}+{\color{#FF8C00}{[3+(t-2)]}}+{\color{#32CD32}{[4+(t-3)]}}+ \cdots+\left[\dfrac{t}{2}+\left(\dfrac{t}{2}+1\right)\right]}_{\frac{t}{2} \, parcelas}\\
&=\underbrace{[1+t]+[1+t]+[1+t]+[1+t]+ \cdots+[1+t]}_{\frac{t}{2} \, parcelas}\\
&=\dfrac{t}{2}\cdot (1+t)\\
&=\dfrac{(1+t)\cdot t}{2}. \end{align*}[/tex]
✓ Se [tex]t[/tex] for ímpar, podemos agrupar os [tex]t[/tex] números [tex]1, \, 2, \, 3, \, 4, \, \ldots \, , \, t[/tex] conforme mostra a figura abaixo, e somá-los.

[tex] \quad\begin{align*} &1+2+3 \cdots+t= {\color{red}{1}}+{\color{#1E90FF}{2}}+{\color{#FF8C00}{3}}+ \cdots+{\color{#FF8C00}{(t-2)}}+{\color{#1E90FF}{(t-1)}}+{\color{red}{t}}=\\
&=\underbrace{{\color{red}{[1+t]}}+{\color{#1E90FF}{[2+(t-1)]}}+{\color{#FF8C00}{[3+(t-2)]}}+ \cdots+{\color{#32CD32}{\left[\dfrac{t-1}{2}+\dfrac{t+3}{2}\right]}}}_{\frac{t-1}{2} \, parcelas}+\dfrac{t+1}{2}\\
&=\underbrace{[1+t]+[1+t]+[1+t]+[1+t]+ \cdots+[1+t]}_{\frac{t-1}{2} \, parcelas}+\dfrac{t+1}{2}\\
&=\dfrac{t-1}{2}\cdot (1+t)+\dfrac{1+t}{2}\\
&=\dfrac{(1+t)\cdot t}{2}. \end{align*}[/tex]
✓ Se [tex]t[/tex] for ímpar, podemos também agrupar de dois em dois, bastando para isso observar que
[tex]\qquad \qquad 1+2+3+4+\cdots +t=0+1+2+3+4+\cdots +t.[/tex]
Perceba que, dessa forma, conseguimos obter a mesma soma com quantidades diferentes de parcelas: do lado esquerdo da igualdade temos [tex]t[/tex] parcelas, ou seja, uma quantidade ímpar de parcelas; mas, do lado direito, temos [tex]t+1[/tex] parcelas, logo, uma quantidade par de parcelas.
Basta então agruparmos as parcelas da soma [tex]0+1+2+3+4+\cdots+t.[/tex]

[tex] \quad\begin{align*}&1+2+3 \cdots+t= 0+1+2+3 \cdots+t=\\
&={\color{red}{0}}+{\color{#1E90FF}{1}}+{\color{#FF8C00}{2}}+{\color{#32CD32}{3}}+ \cdots+{\color{#32CD32}{(t-3)}}+{\color{#FF8C00}{(t-2)}}+{\color{#1E90FF}{(t-1)}}+{\color{red}{t}}\\
&=\underbrace{{\color{red}{[0+t]}}+{\color{#1E90FF}{[1+(t-1)]}}+{\color{#FF8C00}{[2+(t-2)]}}+{\color{#32CD32}{[3+(t-3)]}}+ \cdots+\left[\dfrac{t-1}{2}+\dfrac{t+1}{2}\right]}_{\frac{t+1}{2} \, parcelas}\\
&=\underbrace{[t]+[t]+[t]+[t]+ \cdots+[t]}_{\frac{t+1}{2} \, parcelas}\\
&=\dfrac{t+1}{2}\cdot t\\
&=\dfrac{(1+t)\cdot t}{2}. \end{align*}[/tex]
Um pouco de história
De acordo com um episódio bem pitoresco da História da Matemática, na Alemanha, um garoto de menos de dez anos chamado Gauss surpreendeu seu professor de Matemática ao apresentar rapidamente a resposta ao problema de somar todos os números naturais de 1 a 100.

Extraído da Revista Galileu
O cálculo feito pelo menino Gauss foi:
[tex] \boxed{1+2+3+\cdots +99+100=\dfrac{100}{2} \times 101 = 50\times 101=5050.}[/tex]
Podemos observar que a peripécia do pequeno Gauss é o caso particular de [tex]t=100[/tex] da nossa primeira lousinha, conforme ilustra o esqueminha abaixo.
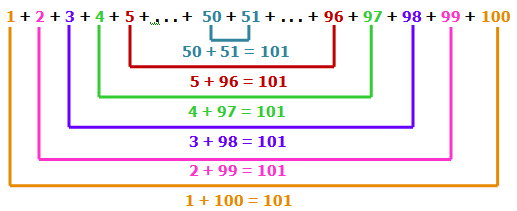
Para a história não ficar sem fim, o menino autor da façanha se tornou um dos mais importantes matemáticos de todos os tempos: Johann Carl Friedrich Gauss, conhecido como o Príncipe da Matemática!
Bem, dizem que uma boa conversa sobre Matemática não pode terminar sem bons problemas…
Assim, aí vão alguns. Divirta-se!
Alguns dos problemas abaixo podem ser resolvidos sem utilizarmos uma soma do tipo [tex]1+2+3+ \cdots + t [/tex].
Mas a ideia aqui é primeiro identificar em cada problema uma soma [tex]1+2+3+ \cdots + t [/tex], para algum [tex]t[/tex] natural, e utilizar a igualdade [tex]1+2+3+ \cdots + t =\dfrac{(1+t)\cdot t}{2}[/tex] para resolvê-lo.
Vamos lá?
Problema 1:
Determine a soma [tex]3+6+9+12+15+\cdots +3000[/tex] dos múltiplos de [tex]3[/tex] menores do que [tex]3001[/tex].
Problema 2:
Determine a seguinte soma, cujas parcelas são números consecutivos: [tex]37+38+39+\cdots + 1405[/tex].
Problema 3:
Qual a soma dos [tex]200[/tex] primeiros números pares positivos?
Problema 4: (UESPI 2012)
No quadro a seguir, são iguais as somas dos elementos de cada uma das linhas, de cada uma das colunas e das diagonais. Além disso, os números que aparecem nos quadrados são os naturais de [tex]1[/tex] até [tex]16[/tex].
[tex]\begin{array}{|c|c|c|c|}
\hline
7&12&A&14\\
\hline
2&B&8&11\\
\hline
16&3&10&D\\
\hline
C&6&15&4\\
\hline
\end{array}[/tex]
Quanto vale [tex]A + B + C + D[/tex]?
Problema 5: (UFBA)
Um relógio que bate de hora em hora o número de vezes correspondente a cada hora baterá, de zero às 12 horas, [tex]x[/tex] vezes.
Calcule o dobro da terça parte de [tex]x[/tex].
Para obter respostas para esses problemas e ouvir a história completa do Gauss,
passe pela Sala de Estudos “A soma [tex]1+2+3+ \cdots+t[/tex]”.
É só clicar AQUI.
Equipe COM – OBMEP
Agosto de 2018.
