.Sala para leitura_008: Simetria, uma breve apresentação

A expressão invertidas, em um contexto qualquer, pode sugerir diferentes interpretações. Uma letra estar invertida, por exemplo, pode significar que a letra está de “cabeça para baixo”, ou em outra posição diferente daquela padrão com a qual estamos acostumados. Entretanto, na condição em que sugere a pergunta, as letras S, E e R parecem estar “refletidas” em relação a uma certa reta. Para ficar mais claro, imagine uma reta vertical, passando bem pelo meio da letra, funcionando como um espelho (ou seja, cada ponto da letra vai para o lado oposto, mantendo a mesma altura e a mesma distância em relação à reta), como ilustra a figura abaixo. Neste caso, a reta em questão comporta-se como eixo de simetria da transformação.

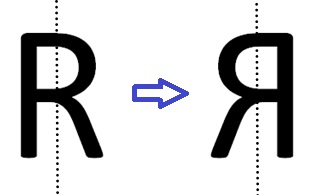
Se uma letra, ou qualquer outro elemento, apresenta o mesmo conjunto de pontos, apenas refletidos, em ambos os lados da reta, então dizemos que este objeto possui uma simetria axial ou simetria bilateral (ou, simplesmente, lateral). Note que o eixo de simetria pode ter qualquer direção. Por exemplo, observamos que a letra E, embora não apresente um eixo de simetria vertical, possui um eixo de simetria horizontal, como ilustra a figura abaixo.

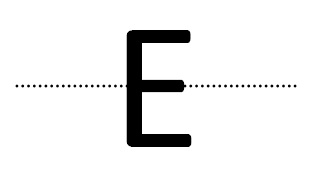
Note que as letras I, M, T e A apresentam simetria lateral (a letra I em duas direções!) e por essa razão, também poderiam ser consideradas invertidas no sentido da pergunta inicial, já que a reflexão de cada uma delas pelo eixo de simetria vertical resulta na própria letra. Assim, podemos concluir que um objeto tem simetria lateral, se sua reflexão por um eixo de simetria resulta nele próprio.

Nesse momento, alguém poderia arriscar-se a dizer que as letras S e R, então, não apresentam simetria…será? De fato, em se tratando de simetria axial, não há simetria em nenhum dos casos. Entretanto, a letra S, em alguns tipos de fonte, pode enquadrar-se numa outra perspectiva de simetria, a simetria central (ou simetria radial), que consiste em uma “rotação” de um elemento em torno de um certo ponto.

A palavra SIMETRIA tem sua origem no grego συμμετρία (de σύν “com” e μέτρον “medida”). A simetria é uma característica que pode ser observada em algumas formas geométricas, equações matemáticas ou outros objetos, ou entidades abstratas, relacionadas com a sua invariância sob certas transformações, movimentos ou trocas.

O seu conceito está relacionado com o de isometria, que é uma transformação geométrica que, aplicada a um objeto, mantém as distâncias entre pontos. Ou seja, os segmentos da figura transformada são geometricamente iguais aos da figura original, podendo variar a direção e o sentido. Exemplos de isometrias são as transformações no plano: rotações, translações e reflexões.

Bacana, hein? E consertando minha resposta, no mínimo três…

Se você também gostou, confira as referências!

Equipe COM – OBMEP