 |
Cada vez mais os meios de comunicação recorrem à Estatística para avaliar e traduzir vários assuntos abordados. |
|
Ah, então é por isso que o estudo dessa parte da Matemática está sendo retomado em nossas escolas… |
 |
 |
Isso mesmo! |
O que são Medidas de Tendência Central
ou Medidas de Centralidade?
A Estatística trabalha com diversas informações que são apresentadas por meio de gráficos e tabelas e com diversos números que representam e caracterizam um determinado conjunto de dados. Dentre todas as informações, podemos retirar valores que representem, de algum modo, todo o conjunto. Esses valores são denominados “Medidas de Tendência Central ou Medidas de Centralidade”.
As medidas de centralidade são a Média Aritmética, a Moda e a Mediana.
Vamos mostrar a seguir o que vem a ser cada uma delas.
É uma das medidas de tendência central mais utilizadas no cotidiano.
É determinada pelo resultado da divisão do somatório dos números dados pela quantidade de números somados.
Por exemplo, vamos determinar a média dos números [tex]3, \, 12, \, 23, \, 15, \, 2[/tex].
Para isso basta somarmos todos os números e dividirmos pela quantidade de números, ou seja:
Média Aritmética=[tex]\dfrac{3+12+23+15+2}{5}=11[/tex]
O cálculo da Média Aritmética é frequentemente usado nas escolas para efetuar a média final dos alunos, em campeonatos de futebol para se obter a média de gols de uma determinada rodada ou mesmo do campeonato; é também utilizado em diversas pesquisas estatísticas, pois determina o direcionamento das ideias expressas em determinados estudos.
Observação: Média Aritmética Ponderada
É uma Média Aritmética na qual alguns dos números envolvidos possuem “pesos”.
Por exemplo, digamos que a média de uma etapa é dada pela média ponderada das notas das três primeiras provas, tomando peso [tex]1[/tex] para a primeira prova, peso [tex]2[/tex] para a segunda prova e peso [tex]3[/tex] para a terceira prova.
Neste caso, a Média Aritmética Ponderada é:
[tex]\dfrac{(1 \times Nota\ 1)+(2 \times Nota\ 2)+(3 \times Nota\ 3)}{1+2+3}[/tex].
Em outras palavras, a Média Aritmética Ponderada é uma Média Aritmética na qual você repete os números tantas vezes quantos são seus pesos.
É a medida de tendência central que consiste no valor observado com mais frequência em um conjunto de dados.
Por exemplo, digamos que o Palmeiras em determinado torneio de futebol fez, em dez partidas, a seguinte quantidade de gols: [tex]5[/tex], [tex]4[/tex], [tex]2[/tex], [tex]1[/tex], [tex]3[/tex], [tex]7[/tex], [tex]1[/tex], [tex]1[/tex], [tex]2[/tex] e [tex]1[/tex].
Para essa sequência de gols marcados, a moda é de [tex]1[/tex] gol, pois é o número que aparece mais vezes.
Outra situação comum seria se dentre [tex]7[/tex] pessoas tomássemos suas idades, a saber: [tex]15[/tex] anos, [tex]20[/tex] anos, [tex]32[/tex] anos, [tex]13[/tex] anos, [tex]5[/tex] anos, [tex]43[/tex] anos e [tex]90[/tex] anos.
Nesse caso, não há moda, pois nenhuma idade se repetiu mais vezes que a outra.
Observação: Quando um conjunto de dados não apresenta moda, dizemos que esse conjunto é amodal.
Caso exista uma moda, denominamos o conjunto de Unimodal.
Existindo duas modas, denominamos o conjunto de bimodal e assim sucessivamente.
É a medida de tendência central que indica exatamente o valor central de um conjunto de dados quando organizados em ordem crescente ou decrescente.
Por exemplo, vamos considerar que um aluno tirou as seguintes notas em cinco provas de uma determinada matéria:
[tex]\qquad \qquad 5[/tex], [tex]8[/tex], [tex]7[/tex], [tex]4[/tex] e [tex]8[/tex].
Colocando as cinco notas em ordem crescente, por exemplo, obtemos [tex]4\lt5\lt7\lt8=8[/tex].
A mediana é o valor que está no centro dessa sequência, ou seja, [tex]7[/tex].
E alguém poderia perguntar: Mas se ao invés de cinco notas fossem seis?
Pois bem, nesse caso ao ordenarmos os números, teremos dois termos centrais ao invés de um. Por exemplo, digamos que as notas agora são:
[tex]\qquad \qquad 5[/tex], [tex]2[/tex] , [tex]8[/tex], [tex]7[/tex], [tex]4[/tex] e [tex]8[/tex].
Colocando em ordem crescente, temos [tex]2\lt4\lt5\lt7\lt8=8[/tex].
Aqui, os dois termos centrais seriam [tex]5[/tex] e [tex]7[/tex]. Portanto, a Mediana desse conjunto de dados é a Média Aritmética dos dois termos centrais, ou seja,
Mediana=[tex]\dfrac{5+7}{2}=6[/tex].
Resumindo o cálculo da Mediana:
- Coloque os valores do conjunto de dados em ordem crescente ou decrescente;
- Se a quantidade de valores do conjunto for ímpar, a mediana é o valor central;
- Se a quantidade de valores do conjunto for par, é preciso tirar a Média Aritmética dos valores centrais.
|
Ainda tenho dúvidas… |

|
Vamos agora ver uma situação bem cotidiana de aplicação do estudo dessas medidas.
O Professor Paulo aplicou uma prova para vinte alunos de uma de suas turmas e agora quer analisar as medidas de tendência central dessas notas.
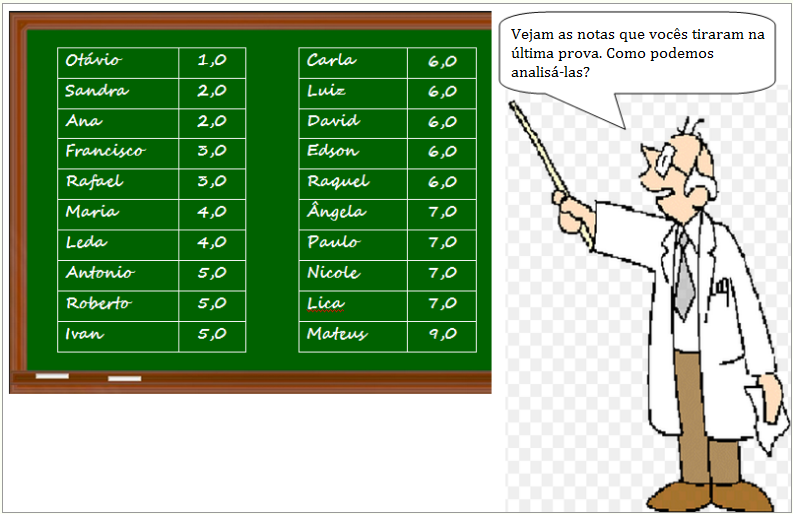
1) Vamos calcular, primeiro, a Média Aritmética das notas.
Para tanto, basta somarmos todas as notas e dividirmos por [tex]20[/tex]. Deste modo, temos:
Média Aritmética=[tex]\dfrac{101}{20}=5,05[/tex].
É importante observarmos que com a média aritmética cada aluno pode comparar a sua nota em relação à nota da turma como um todo. De uma forma mais geral, podemos afirmar que [tex]10[/tex] alunos ficaram abaixo da média e [tex]10[/tex] alunos ficaram acima da média.
2) Vamos calcular, agora, a Mediana. Observe que as notas já estão classificadas em ordem crescente no quadro, o que facilita a identificação da mediana.
Deste modo, a mediana das [tex]20[/tex] notas é a média aritmética das [tex]10^a[/tex] e [tex]11^a[/tex] notas, ou seja,
Mediana=[tex]\dfrac{5+6}{2}=5,5[/tex].
Com a mediana é possível saber se a turma teve ou não um bom desempenho:
uma mediana alta é sinônimo de bom rendimento da turma; mas se a mesma for baixa, é sinônimo de um baixo rendimento da turma.
3) Já em relação à Moda, esse conjunto de dados possui Moda [tex]6[/tex], pois essa é a nota que mais ocorre: cinco vezes.
Setembro de 2017.
 |
Esperamos que você tire proveito da explanação feita aqui. |
Equipe COM – OBMEP
