Problema
Em um triângulo retângulo, a hipotenusa mede 49 cm e a altura relativa à hipotenusa mede 16 cm.
Calcule, em centímetros, a soma dos comprimentos dos catetos desse triângulo.
Solução 1
Na figura abaixo, o triângulo [tex]ABC[/tex] é retângulo em [tex]B[/tex], a altura relativa hipotenusa é [tex]{BP}=16[/tex], [tex]{AB}=a[/tex] e [tex]{BC}=b[/tex].
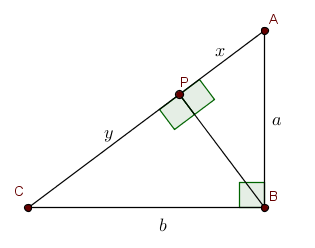
Agora, observe que [tex]\triangle{APB}[/tex] e [tex]\triangle{ABC}[/tex] são triângulos semelhantes, pois possuem um ângulo em comum, o [tex]\measuredangle{PAB}[/tex], e possuem um ângulo reto.
Assim:
[tex]\qquad \dfrac{a}{49} = \dfrac{16}{b}[/tex],
donde
[tex]\qquad ab = 784[/tex].
Pelo Teorema de Pitágoras, podemos escrever que
[tex]\qquad a^2 + b^2 = 2401[/tex],
logo
[tex]\qquad (a+b)^2 = 2401 + 2ab[/tex],
ou seja,
[tex]\qquad (a+b)^2 = 3969[/tex]
e, finalmente,
[tex]\qquad a+b=63\, [/tex]cm.
Solução elaborada pelo aluno do PIC-OBMEP Angelo Donizeti Lorenconi Junior, com contribuições dos Moderadores do Blog.
Solução 2

Com base na figura acima podemos comparar as áreas dos três triângulos e observar que [tex]\, A_{\triangle{APB}}+A_{\triangle{CPB}}=A_{\triangle{ABC}}[/tex].
Assim, segue que:
[tex]\qquad \dfrac{16x}{2}+\dfrac{16y}{2}=\dfrac{ba}{2}[/tex]
[tex]\qquad 16x+16y=ba[/tex]
[tex]\qquad 16(x+y)=ba[/tex]
[tex]\qquad 16\cdot{49}=ba[/tex]
[tex]\qquad ba=784[/tex].
Pelo Teorema de Pitágoras temos que
[tex]\qquad a^2 + b^2 =49^2= 2401[/tex]
e, por outro lado,
[tex]\qquad (a+b)^2=a^2 + 2ab+b^2[/tex].
Assim,
[tex]\qquad (a+b)^2 = 2401 + 2ab=2401+2\cdot 784[/tex],
ou seja,
[tex]\qquad (a+b)^2 = 3969[/tex]
e, finalmente,
[tex]\qquad a+b=63[/tex].
Portanto, a soma dos catetos do triângulo [tex]ABC[/tex] é [tex]63\, [/tex]cm.
Solução elaborada pela aluna do PIC-OBMEP Larissa Bonadiman Grassi, com contribuições dos Moderadores do Blog.
Solução 3

A área do triângulo [tex]ABC[/tex] é [tex]\dfrac{49\times 16}{2}[/tex], ou seja, [tex]392\, \text{cm}^2[/tex].
Por outro lado, essa área é definida por [tex]\dfrac{ab}{2}[/tex], sendo [tex]a[/tex] e [tex]b[/tex] as medidas dos catetos, uma vez que o triângulo é retângulo, assim:
[tex]\qquad \dfrac{ab}{2}=392[/tex],
donde
[tex]\qquad ab=784[/tex].
Veja que, pelo Teorema de Pitágoras,
[tex]\qquad a^2+b^2=49^2=2401[/tex]
mas, por outro lado,
[tex]\qquad (a+b)^2=a^2+b^2+2ab[/tex],
dessa forma,
[tex]\qquad (a+b)^2=(a^2+b^2)+2ab=2401+2\cdot 784=3969[/tex],
donde,
[tex]\qquad (a+b)=\sqrt{3969}=\fbox{63}[/tex].
Finalmente,
[tex]\qquad a+b=63[/tex]
e, portanto, a soma dos catetos do triângulo [tex]ABC[/tex] é [tex]63\, [/tex]cm.
Solução elaborada pela aluna do PIC-OBMEP Noemi Zeraick Monteiro, com contribuições dos Moderadores do Blog.
