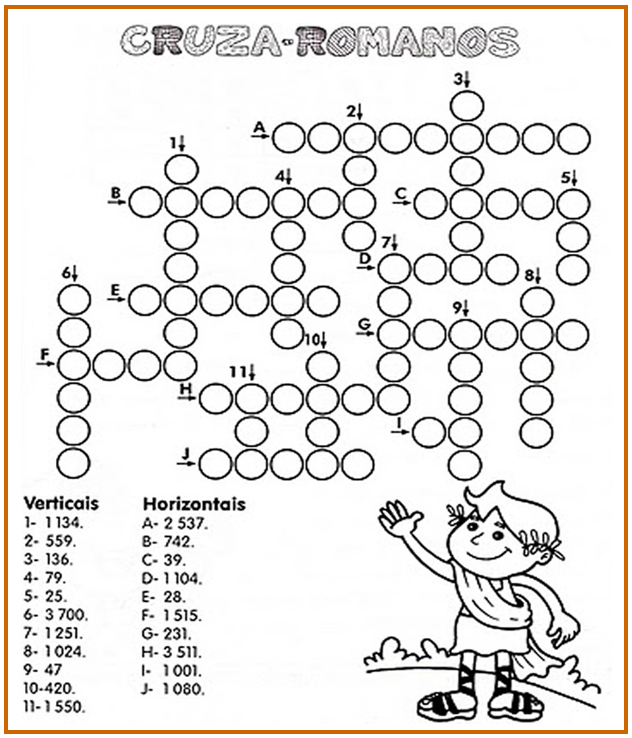
Número é um conceito abstrato que representa a ideia de quantidade e que, portanto, sempre esteve presente na organização da vida humana.
A necessidade do uso dos números pelo homem fez com que, ao longo de vários séculos, eles passassem por diversas mudanças na maneira de serem representados. Com a evolução dessa representação, convencionou-se chamar de um sistema de numeração ao conjunto dos símbolos utilizados para representar quantidades e das regras que definem a forma dessa representação.
Levou-se muito tempo para que o sistema de representação dos números fosse esse que hoje utilizamos e, para isso, várias civilizações desenvolveram sistemas de numeração próprios. O tema central desta Sala de Estudos é um dos sistemas de numeração desenvolvidos por civilizações antigas: o Sistema de Numeração Romano .
Embora os algarismos romanos tenham sido desenvolvidos há mais de 2.000 anos, ainda nos dias de hoje não é difícil encontrá-los em mostradores de relógios, na numeração de Artigos de documentos ou de capítulos de livros, diferenciando papas, rainhas e reis com o mesmo nome (Rei Luís XV, Papa Paulo VI), na identificação de séculos, entre outras situações.
Vocês saberiam dizer como surgiram os algarismos romanos?
Os algarismos romanos são originários da Roma Antiga. Foram desenvolvidos como uma forma de identificação matemática simples e usados praticamente em todo o Império Romano. Esse sistema é composto de apenas sete símbolos que, atualmente, correspondem a letras maiúsculas do nosso alfabeto; a saber: [tex]I, V, X, L, C, D[/tex] e [tex]M[/tex].
No livro [tex]50[/tex] IDEIAS DE MATEMÁTICA QUE VOCÊ PRECISA CONHECER, foi sugerido que o uso dos símbolos [tex]I, II, III, IIII[/tex] derivou da aparência dos dedos e o símbolo [tex]V[/tex] do formato da mão aberta.
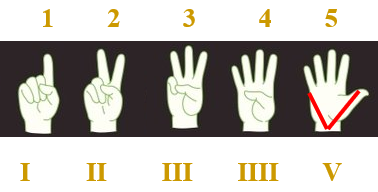

Se você estranhou a representação do número [tex]4[/tex] mostrada acima, saiba que esta é uma curiosidade desse sistema. Hoje a representação do [tex]4[/tex] no sistema dos algarismos romanos é conhecida no mundo todo como sendo [tex]IV[/tex], mas há registros que mostram uma forma de representação diferenciada mais arcaica: [tex]IIII[/tex]. Esta última, apesar de pouco conhecida, é muito vista em relógios que costumam apresentar as horas por meio de algarismos romanos.
(Sobre esse fato, aprofunde seu conhecimento lendo o texto deste link.)
O símbolo [tex]X[/tex], por sua vez, parece ter sido obtido da junção de dois símbolos [tex]V[/tex], com um deles invertidos, obtendo-se, assim, duas mãos ou dez dedos.
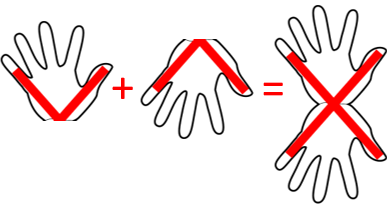
Outro fato curioso é que os romanos não conheciam o zero, que só veio a ser introduzido na Matemática muito tempo depois, pelos hindus/árabes. Dessa forma, os romanos não tinham uma representação para o zero em seu sistema de numeração. Para eles o numeral de menor valor era o [tex]1.[/tex]
Curiosidade Histórica

Um registro da forma não usual de representar o número [tex]4[/tex] como [tex]IIII[/tex] aconteceu com o nome do Luís, o décimo quarto rei da França, hoje universalmente conhecido como Luís [tex]XIV[/tex].
Na verdade, ele preferia ser conhecido como Luís [tex]XIIII[/tex] e fez uma lei para que todos os relógios mostrassem as [tex]4[/tex] horas como [tex]IIII[/tex] horas.
O sistema romano, diferentemente de outros sistemas de numeração, utiliza apenas os seguintes símbolos:

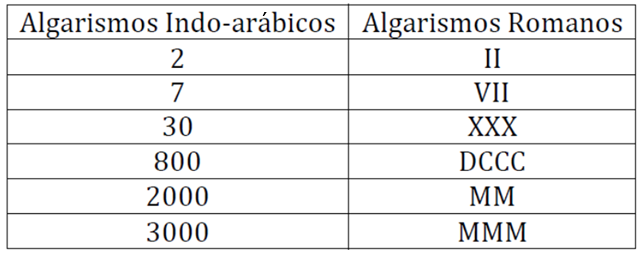
Tendo como base esses sete símbolos, os romanos desenvolveram regras específicas de agrupamentos, originando um sistema numérico próprio. A comparação com os algarismos indo-arábicos [tex](1, 2, 3, \cdots)[/tex] permite entender melhor essas regras.
No sistema indo-arábico, de acordo com a posição ocupada, um mesmo algarismo assume valores diferentes. No sistema numérico romano, as regras diferem consideravelmente.
Vejamos!
Regras para Numeração Romana – Parte 1
As três primeiras regras que abordaremos são utilizadas para a escrita dos números de [tex]1[/tex] a [tex]3999[/tex].
Regra 1
Quando agrupamos símbolos à direita de outros iguais ou de maior valor, adicionamos seus valores. Observem os exemplos do próximo quadro.

Regra 2
Quando agrupamos símbolos à esquerda de outros que tenham maior valor, subtraímos os respectivos valores, desde que sejam observados os seguintes casos:
► Os símbolos [tex]M[/tex] e [tex]D[/tex] admitem somente subtração do valor do símbolo [tex]C[/tex];
► Os símbolos [tex]C[/tex] e [tex]L[/tex] admitem somente subtração do valor do símbolo [tex]X[/tex];
► Os símbolos [tex]X[/tex] e [tex]V[/tex] admitem somente subtração do valor do símbolo [tex]I[/tex].
Vejam os exemplos no quadro a seguir.

Regra 3
Na formação dos algarismos romanos, alguns símbolos podem ser repetidos, sucessivamente, até 3 vezes seguidas.
Para cada um dos símbolos [tex]I, X[/tex] e [tex]C[/tex], a repetição só é possível se apenas eles aparecerem na representação ou quando colocados à direita de um símbolo de maior valor. O símbolo [tex]M[/tex] pode ser repetido. Símbolos colocados à esquerda de um símbolo de maior valor não podem se repetir. Dessa forma, os romanos evitavam que um mesmo número do sistema fosse representado por um agrupamento aleatório de símbolos. Os símbolos [tex]V, L[/tex] e [tex]D[/tex] não podem aparecer repetidos. Veja alguns exemplos.

Agora, com base no exposto, como representamos
o número [tex]3555[/tex] em algarismos romanos?
Inicialmente, observem que o número [tex]3555[/tex] corresponde à soma dos números [tex]3000[/tex], [tex]500[/tex], [tex]50[/tex] e [tex]5[/tex]. Deste modo, o [tex]3555[/tex] em algarismos romanos seria a junção dos símbolos [tex]MMM[/tex] com o símbolo [tex]D[/tex] mais o [tex]L[/tex] e, finalmente, o [tex]V.[/tex] Assim, obtemos a seguinte representação: [tex]MMMDLV.[/tex]
Continuando…
Regras para Numeração Romana – Parte 2
Agora, veremos regras para números acima de [tex]3999[/tex].
Regra 4
Para números indo-arábicos a partir de [tex]4000[/tex], foi estabelecido um símbolo convencional chamado vinculum (plural: vincula): um traço horizontal que, quando colocado sobre um ou mais símbolos, indica que o valor numérico do(s) símbolo(s) abaixo dele será multiplicado por mil. Desse modo, utiliza-se [tex]\overline{IV}[/tex] para representar [tex]4000[/tex]; [tex]\overline{V}[/tex] para [tex]5000[/tex]; [tex]\overline{XX}[/tex] para [tex]20000[/tex] e assim por diante.
Regra 5
Para números na casa dos milhões, bilhões, trilhões, [tex]\cdots[/tex], o símbolo receberá tantos vincula quantos forem necessários.
Por exemplo, como [tex]M[/tex] já equivale a [tex]1000[/tex], ele receberá apenas um vinculum para representar [tex]1000000[/tex], enquanto [tex]V[/tex] receberá dois vincula para indicar [tex]5000000[/tex] e assim sucessivamente.
Exemplos
[tex] \, 10340[/tex]
Observem que [tex]10340[/tex] é o mesmo que [tex]10000+300+40[/tex]. Portanto, basta escrevermos o [tex]10000=\overline{X}[/tex], seguido do [tex]300=CCC[/tex] e do [tex]40=XL:[/tex] [tex]\overline{X}CCCXL \, .[/tex]
[tex] \, 87990000[/tex]
Veja que [tex]87990000[/tex] é o mesmo que [tex]87000000+990000[/tex]. Portanto, basta escrevermos o [tex]87000000=\overline{\overline{LXXXVII}}[/tex], seguido do [tex]990\ 000=\overline{CMXC} [/tex], ou seja, [tex]\overline{\overline{LXXXVII}}\overline{CMXC} \, .[/tex]
 |
Clicando AQUI, você terá acesso a uma tabela com numerais romanos de [tex]I[/tex] a [tex]M[/tex]. |
Que tal você resolver alguns problemas para ajudar no entendimento das regras para se escrever números utilizando algarismos romanos?
É só clicar no botão abaixo e
Boa diversão!
Operando com algarismos romanos
Um probleminha
Efetue a seguinte adição: [tex] \, \, CCXIX + XLVII.[/tex]
Se você fosse resolver o probleminha proposto provavelmente transformaria os dois valores a serem somados para o nosso sistema usual de numeração, efetuaria a continha e converteria o resultado para algarismos romanos:
[tex]CCXIX + XLVII \, \textcolor{#8B5A2B}{ \, \xmapsto [\text {sistema e fazer a conta}] {\text {converter para o nosso sistema}}} \, 219+47=266 \\
\,[/tex]
[tex]\, \\
\qquad \qquad 266 \textcolor{#8B5A2B}{\xmapsto [\text {para algarismos romanos}] {\text {converter o resultado }}} \, CCLXVI [/tex]
Mas será que é possível desenvolver essa adição manipulando diretamente os símbolos romanos?
E as outras três operações básicas, Subtração; Multiplicação; Divisão, é possível efetuá-las pensando apenas em termos dos numerais romanos?
Se você ficou curioso(a), clique nos botões abaixo: vamos apresentar algoritmos simples que nos permitem somar, subtrair, multiplicar e dividir números que hoje chamamos de “números naturais não nulos” utilizando o sistema romano de numeração.
Sugerimos fortemente que você siga a ordem na qual as operações foram anunciadas: Adição; Subtração; Multiplicação; Divisão.
Bons Estudos!
 |
Clicando AQUI, você terá acesso a várias atividades com algarismos romanos. |
Equipe COM – OBMEP
Fevereiro de 2019.
[1] CRILLY, Tony. 50 ideias de matemática que você precisa conhecer. (Original: 50 maths ideas you really need to know). São Paulo: Planeta, 2017.
[2] Revista do Professor de Matemática 5 – página 46 – Algarismos Romanos – Uma aula diferente – Márcia de Oliveira Rebello e Rosângela Tortora
[3] https://www.colegioweb.com.br/matematica/origem-dos-numeros-romanos.html (Último acesso em 23/06/20)
[5] Escola Educação (Último acesso em 23/06/20)
[6] Roman Arithmetic (Último acesso em 23/02/19)