✏ Link da Sala para dispositivos da Apple.
Valor Esperado e Aplicações
Nesta Sala, apresentaremos uma ferramenta matemática para avaliar muitas questões do mundo real relacionadas a eventos aleatórios como, por exemplo, jogos de azar, seguros, investimentos em eventos futuros, etc.
Esta ferramenta é o conceito de valor esperado, também chamado de esperança matemática, que é muito importante no estudo de probabilidades, além de possuir aplicações a outros ramos científicos. E, apesar da grande variedade de aplicações, o valor esperado é um conceito surpreendentemente simples!
Adotaremos como condição para uma leitura satisfatória desta Sala o conhecimento da teoria básica das Probabilidades.
Experimento Aleatório e Probabilidades
Iniciaremos o nosso estudo com uma pequena revisão sobre alguns conceitos básicos da Teoria das Probabilidades. Caso você ainda não tenha estudado um pouco desse assunto, sugerimos a leitura da sala Probabilidades do nosso Blog, na qual você vai encontrar um estudo mais detalhado dessa teoria.
– O resultado não pode ser previsto com certeza.
– Embora não seja possível afirmar que resultado em particular ocorrerá, é possível descrever o conjunto de todos os resultados possíveis do experimento.
► Espaço Amostral: conjunto formado por todos os possíveis resultados de um experimento ou fenômeno aleatório. Neste texto, indicaremos esse conjunto pela letra grega maiúscula ômega, [tex]\Omega[/tex], e trabalharemos quase sempre com experimentos aleatórios cujos respectivos espaços amostrais sejam finitos (veja o exemplo do lançamento do dado abaixo).
► Evento: qualquer subconjunto do espaço amostral. Os eventos geralmente são indicados por letras maiúsculas do nosso alfabeto, indexadas ou não; e, na prática, dizemos que um evento [tex]E[/tex] ocorre se, quando realizado o experimento, obtém-se um resultado que pertence a [tex]E[/tex]. Dentro de um mesmo espaço amostral, quando a ocorrência de um evento [tex]E_1[/tex] impossibilita a ocorrência de outro evento [tex]E_2[/tex], dizemos que os eventos são mutuamente excludentes ou disjuntos.
Por exemplo, lançar um dado cujas faces estão numeradas de [tex]1[/tex] a [tex]6[/tex] e verificar a numeração da face voltada para cima é um experimento aleatório. O espaço amostral para este experimento será [tex] \Omega=\{1, 2, 3, 4, 5, 6\}.[/tex] Sortear um número maior do que [tex]4[/tex] será o evento [tex]E=\{5, 6\}\subset \Omega=\{1, 2, 3, 4, 5, 6\}.[/tex] Observe que o mesmo lançamento do dado pode dar origem a um experimento aleatório diferente, por exemplo, lançar um dado cujas faces estão numeradas de [tex]1[/tex] a [tex]6[/tex] e verificar a paridade do resultado da face voltada para cima é um experimento aleatório diferente cujo espaço amostral é [tex] \Omega’=\{\text{número par}, \text{número ímpar} \}.[/tex]
► Probabilidade clássica: Suponha um experimento aleatório cujo espaço amostral [tex]\Omega[/tex] é finito e equiprovável, ou seja, [tex]\Omega[/tex] é formado por um número finito de resultados igualmente prováveis. Se [tex]E[/tex] é um evento qualquer do espaço amostral [tex]\Omega[/tex], a probabilidade de [tex]E [/tex] ocorrer, ou simplesmente a probabilidade do evento [tex]E[/tex], é definida como a razão entre o número de elementos de [tex]E[/tex] e o número de elementos de [tex]\Omega[/tex]. Em símbolos,
[tex]\qquad \qquad P(E)=\dfrac{n(E)}{n(\Omega)},[/tex]
sendo [tex]n(E)[/tex] o número de elementos do evento e [tex]n(\Omega)[/tex] o número de elementos do espaço amostral.
► Probabilidade Frequencial: Considere um experimento aleatório com espaço amostral [tex]\Omega[/tex]. Suponhamos que esse experimento seja repetido nas mesmas condições [tex]n[/tex] vezes e o evento [tex]E[/tex] ocorra exatamente [tex]m[/tex] vezes. Então, a frequência relativa de vezes que o evento [tex]E[/tex] ocorreu, ou simplesmente a frequência relativa de [tex]E[/tex], é denotada por [tex]fr(E)[/tex] e assim definida:
[tex]\qquad \qquad fr(E)=\dfrac{m}{n}.[/tex]
A probabilidade frequencial de [tex]E[/tex] é definida como o número [tex]P(E)[/tex] para o qual as frequências relativas [tex]fr(E[/tex]) se aproximam quando vamos aumentando cada vez mais o número [tex]n[/tex] de vezes que realizamos o experimento.
Deve-se notar que as frequências relativas do evento [tex]E[/tex] são aproximações da probabilidade [tex]P(E)[/tex]. As duas se igualam apenas no limite de infinitos experimentos. Em geral, para um valor de [tex]n[/tex] razoavelmente grande, [tex]fr(E)[/tex] é uma boa aproximação para [tex]P(E)[/tex]. Podemos até pensar que temos duas probabilidades diferentes para um evento [tex]E[/tex]: a probabilidade clássica e a probabilidade frequencial. Mas, pode-se provar que, quando um evento [tex]E[/tex] tem probabilidade clássica [tex]P(E)[/tex], então o número do qual as frequências relativas se aproximam é exatamente [tex]P(E)[/tex]. Esse resultado é conhecido como Lei dos Grandes Números.
Vamos ilustrar a importância do conceito de probabilidade frequencial apresentando algumas de suas inúmeras aplicações práticas. A primeira dessas aplicações está relacionada a eventos aleatórios com espaço amostral finito e equiprovável, mas que por razões práticas temos dificuldades de descrever tal espaço amostral. A segunda aplicação irá ilustrar o uso da probabilidade frequencial em espaços amostrais infinitos nos quais não podemos fazer uso da definição clássica de probabilidade.
 Imagem extraída do site do Freepik.(Acesso em 14/04/2024.)
Imagem extraída do site do Freepik.(Acesso em 14/04/2024.)
Uma estratégia consiste em capturar um número [tex]q[/tex] de peixes com uma rede, marcá-los e reintroduzi-los no lago.
Agora, vamos considerar “o experimento aleatório de capturar algum peixe desse lago”.
O espaço amostral para esse evento será o conjunto [tex]\Omega[/tex] contendo todos os [tex]Q[/tex] peixes. Vamos fazer a suposição que cada um dos peixes do lago tem a mesma chance de ser capturado. Assim, nosso espaço amostral [tex]\Omega[/tex] será finito e equiprovável.
Consideremos o evento [tex]E=\{ \mathrm{peixes \ marcados }\}[/tex]; pela definição clássica de probabilidade, temos
[tex]\qquad P(E)=\dfrac{n(E)}{n(\Omega)}=\dfrac{q}{Q},[/tex]
ou seja,
[tex] \qquad Q=\dfrac{q}{P(E)}.[/tex]
Assim, se soubéssemos o valor de [tex]P(E)[/tex], teríamos nossa fórmula para calcular [tex]Q[/tex]. Entretanto, sem o conhecimento da quantidade de peixes, não poderemos aplicar a definição clássica. Aqui, portanto, será útil a fórmula frequencial.
Note que, por meio da captura de um número [tex]n[/tex] razoavelmente grande de peixes, podemos calcular o valor [tex]fr(E)[/tex] que, pela Lei dos Grandes Números, será uma aproximação para [tex]P(E)[/tex]. Logo,
[tex]\qquad \boxed{Q\approx \dfrac{q}{fr(E)}}.[/tex]
Essa fórmula é muito usada por ecologistas para se estimar o tamanho de populações de certas espécies.
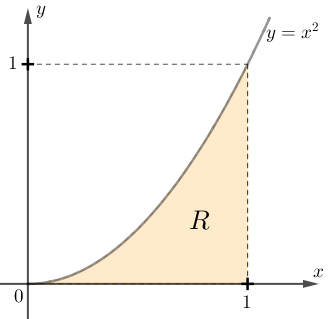
Existem ferramentas que permitem o cálculo exato dessa área, como o cálculo integral que geralmente é estudado em cursos de Ciências Exatas. Mas, existe uma maneira bem interessante de aproximar o valor dessa área com o uso de probabilidades.
Consideremos, então, o quadrado unitário da figura abaixo e o experimento “selecionar aleatoriamente um ponto desse quadrado”.
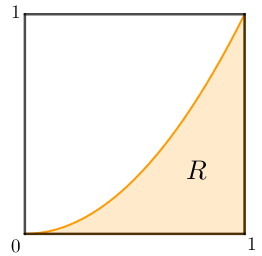
Este será um experimento aleatório com espaço amostral infinito, já que este consistirá de todos os pontos do quadrado. Seja [tex]E[/tex] o evento “selecionar um ponto na região [tex]R[/tex]”. É intuitivo aceitar que
[tex]\qquad P(E)=\dfrac{\mathrm{Área}(R)}{ \mathrm{Área(Quadrado)}}=\mathrm{Área}(R),\\
~~[/tex]
já que [tex] \mathrm{Área(Quadrado)} =1[/tex].
Não sabemos como calcular a área da região [tex]R[/tex] e também não podemos aplicar a definição clássica de probabilidades para calcular [tex]P(E)[/tex], já que o espaço amostral é infinito. O que nos resta? Probabilidade frequencial. Um experimento feito com apenas [tex]100[/tex] pontos teve o resultado apresentado na próxima figura.
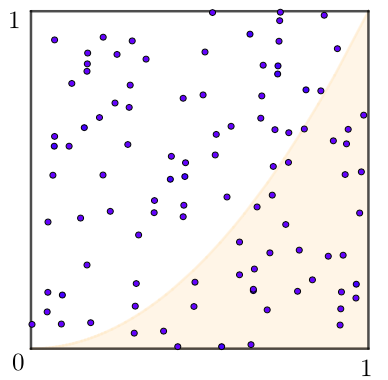
Das [tex]100[/tex] vezes que o experimento foi realizado, o evento [tex]E[/tex], que consiste em obter um ponto na região [tex]R[/tex], ocorreu [tex]35[/tex] vezes. Como [tex]fr(E)\approx P(E[/tex]), então:
[tex]\qquad \mathrm{Área}(R)=P(E)\approx fr(E)=\dfrac{35}{100}=0,35.[/tex]
Por curiosidade, [tex] \mathrm{Área}(R)=1/3=0,33…[/tex]
Observe que com apenas [tex]100[/tex] pontos, obtivemos uma boa aproximação. Imaginem com milhares ou milhões de pontos, o que pode ser facilmente executado com o auxílio de um computador.
Os dois exemplos que acabamos de apresentar sobre o uso da probabilidade frequencial são aplicações do Método de Monte Carlo, desenvolvido pelo grande matemático e físico polaco Stanislaw Ulam (1909-1984).
Como ficará claro mais adiante, esses exemplos podem ser interpretados como aplicações do conceito de valor esperado.
Valor Esperado ou Esperança
Embora os resultados de experimentos aleatórios não possam ser previstos com certeza, pode ser possível estimar o que se espera a longo prazo desses experimentos.
- Se o experimento aleatório tem espaço amostral finito e equiprovável, podemos utilizar Probabilidade Clássica para estimar particularmente as possibilidades de ocorrência dos eventos desse experimento, sem nem mesmo repeti-lo várias vezes.
- Se for possível repetir o experimento um número bem grande de vezes, podemos utilizar o conceito de frequência relativa para estimar as possibilidades de ocorrência dos seus eventos.
Mas e quando, mesmo com essas probabilidades aplicadas no modelo matemático de um experimento, não conseguirmos “prever” o futuro?
Por exemplo, suponha a seguinte situação:
- Seu João se diverte muito com a rotina diária de, ao caminho de seu trabalho, fazer uma aposta na banquinha da dona Mariazinha, que fica na praça em frente ao local de trabalho dele.
- Um baralho completo (4 naipes com 13 cartas) é embaralhado e, sem olhar, seu João retira uma carta.
Se a carta retirada for um Rei, seu João ganha R$ 10,00.
Se a carta retirada não for um Rei, seu João paga R$ 1,00 para dona Mariazinha.
O jogo no qual ele aposta é o seguinte:
É claro que em um determinado dia seu João pode ganhar ou perder; mas, a longo prazo, qual é o resultado esperado para as apostas do seu João?
Veja que, como existem 4 Reis entre as 52 cartas do baralho, a probabilidade de seu João retirar um Rei é [tex]\dfrac{4}{52}[/tex]; e a probabilidade de sair outra carta é [tex]\dfrac{52-4}{52}=\dfrac{48}{52}.[/tex] Mas e daí?
Observe que, multiplicando o ganho e a perda pela respectiva probabilidade disso acontecer e somando os produtos obtidos, obtemos:
[tex]\qquad \textcolor{blue}{10 \times \dfrac{4}{52}}+\textcolor{red}{(-1) \times \dfrac{48}{52}}\approx -0,15 [/tex]
e assim o valor médio esperado é uma perda de aproximadamente 0,15 reais.
É claro que seu João faz a aposta diariamente porque ele se diverte e é uma maneira de ajudar a dona Mariazinha.
O valor [tex]-0,15 [/tex] obtido é o objeto que vamos definir formalmente. Observe que nos nossos cálculos, a cada evento do experimento aleatório “Fazer uma aposta”, [tex]E_1:GANHAR[/tex] e [tex]E_2:PERDER[/tex], associamos um número real, [tex]e_1=10[/tex] e [tex]e_2=-1[/tex] respectivamente, e as respectivas probabilidades, [tex]p_1=\dfrac{4}{52}[/tex] e [tex]p_2=\dfrac{48}{52}.[/tex]
De modo geral, serão estes os valores numéricos que associaremos aos eventos do experimento que vamos calcular o valor médio de um experimento aleatório a longo prazo!
[tex]\quad \Omega=\{(cara,cara);(cara,coroa);(coroa,cara);(coroa,coroa)\}.[/tex]
Podemos associar a cada elemento de [tex]\Omega[/tex] o número de caras obtidas ou, dependendo do que está sendo analisado, poderíamos associar o número de coroas.
Com essa observação, já temos condição de definir o objeto central desta Sala.
- Definição: Seja [tex]E[/tex] um experimento aleatório cujo espaço amostral finito [tex]\Omega[/tex], não necessariamente equiprovável, pode ser escrito como união de eventos dois a dois disjuntos, ou seja, [tex]\Omega=E_1 \cup E_2 \cup \dots \cup E_k,[/tex] com [tex]E_i\cap E_j=\emptyset[/tex], para [tex] i\neq j[/tex].
Sejam também [tex]e_1, e_2, \dots, e_k[/tex] números reais não necessariamente distintos que, de alguma forma, caracterizam numérica e respectivamente os eventos [tex]E_1 , E_2 , \dots , E_k[/tex]; e [tex]P\left(E_1\right) , P\left(E_2\right) , \dots ,P\left(E_k\right)[/tex] as respectivas probabilidades desses eventos.
Para a associação
- número real [tex]e_1[/tex] associado ao evento [tex] E_1[/tex], número real [tex]e_2[/tex] associado ao evento [tex]E_2[/tex] e, assim sucessivamente, até o número [tex]e_k[/tex] associado ao evento [tex]E_k[/tex],
o valor esperado do experimento aleatório [tex]E[/tex] é o número definido e denotado como se segue:
[tex]\qquad \qquad \boxed{VE=e_1\cdot P(E_1) +e_2\cdot P(E_2)+ \dots +e_k\cdot P(E_k)^{~}_{~}}.[/tex]
Veja que o número [tex]VE[/tex] depende do experimento aleatório em questão e também da associação entre os eventos [tex]E_1, E_2, \dots, E_k~ [/tex] e os números [tex]~e_1, e_2, \dots, e_k[/tex].
Vamos tentar entender o significado do número [tex]VE[/tex] utilizando mais um exemplo.
Que numeração será essa?”
Bem, sabemos que o espaço amostral [tex]\Omega=\{1, 2, 3, 4, 5, 6\}[/tex] deste experimento é finito e equiprovável. Podemos fazer a decomposição
[tex]\quad \Omega=E_1\cup E_2 \cup E_3\cup E_4 \cup E_5 \cup E_6, [/tex]
sendo
[tex]\quad E_1=\{1\}[/tex], [tex]E_2=\{2\}[/tex], [tex]E_3=\{3\}[/tex], [tex]E_4=\{4\}[/tex], [tex]E_5=\{5\}[/tex] e [tex]E_6=\{6\}.[/tex]
Como o dado é honesto, temos que [tex]P(E_1)=P(E_2)=P(E_3)=P(E_4)=P(E_5)=P(E_6)=\dfrac{1}{6}.[/tex]
Assim, com a seguinte associação,
[tex]\qquad E_1 \to 1[/tex] ; [tex]E_2 \to 2[/tex] ; [tex]E_3 \to 3[/tex] ; [tex]E_4 \to 4[/tex] ; [tex]E_5 \to 5[/tex] ; [tex]E_6 \to 6[/tex],
o valor esperado do experimento [tex]E[/tex] será:
[tex]\qquad VE=1 \cdot \dfrac{1}{6}+2 \cdot \dfrac{1}{6}+3 \cdot \dfrac{1}{6}+4 \cdot \dfrac{1}{6}+5 \cdot \dfrac{1}{6}+6 \cdot \dfrac{1}{6}=3,5.[/tex]
Mas qual é o significado do valor [tex] VE=3,5[/tex], uma vez que no dado não existe uma face com o número [tex]3,5[/tex]?
Para compreendermos esse número, vamos realizar uma experiência: Vamos lançar um dado [tex]n[/tex] vezes e somar, inicialmente, todos os números obtidos, formando a soma [tex]S_n.[/tex] Por exemplo, se para três lançamentos os resultados forem [tex]5, 4[/tex] e [tex] 2[/tex], então teremos [tex]S_3=11.[/tex]
Observem alguns valores obtidos para a soma [tex]S_n[/tex], em função de [tex]n[/tex], em dez experiências com lançamentos de um dado que realizamos:
[tex]\quad S_{20}=72, ~ S_{40}=150, ~ S_{60}=219, ~ S_{80}=282, ~ S_{100}=357,[/tex]
[tex]\quad S_{120}=432, ~ S_{140}=499, ~ S_{160}=563, ~S_{180}=633, ~ S_{200}=702. [/tex]
Vamos agora calcular as respectivas “médias das somas [tex]S_n[/tex]” obtidas, ou seja, vamos calcular a razão [tex]\dfrac{S_n}{n}[/tex], para os dez valores de [tex]n[/tex] utilizados:
[tex]\quad\frac{S_{20}}{20}=3,6,~\frac{S_{40}}{40}=3,75,~ \frac{S_{60}}{60}=3,65,~ \frac{S_{80}}{80}=3,52,~ \frac{S_{100}}{100}=3,57,\\
~~\\
\quad\frac{S_{120}}{120}=3,6,~\frac{S_{140}}{140}=3,564,~ \frac{S_{160}}{160}=3,518,~ \frac{S_{180}}{180}=3,516,~\frac{S_{200}}{200}=3,51.\\
~~[/tex]
Podemos representar, em um gráfico cartesiano, [tex]\dfrac{S_n}{n}[/tex] como função de [tex]n:[/tex]
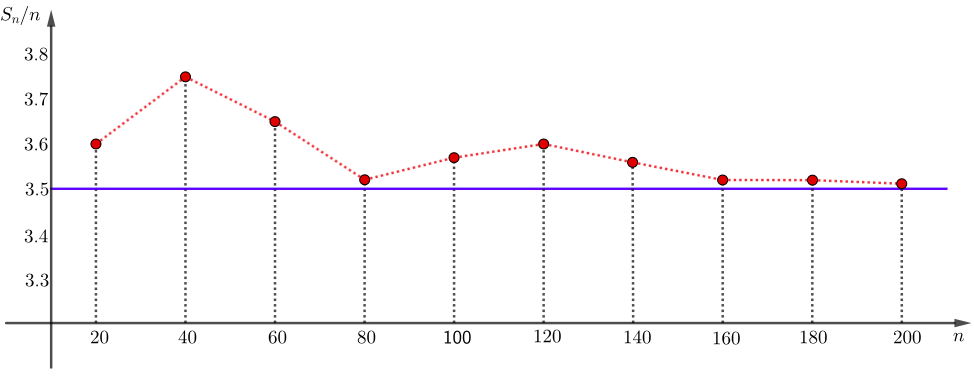
Note que, à medida que o valor de [tex]n[/tex] cresce, as médias das somas, [tex] \dfrac{S_n}{n}[/tex], se aproximam do valor esperado [tex]3,5.[/tex]
Com apenas [tex]200[/tex] lançamentos, tivemos uma média de [tex]3,51.[/tex] E esse número será cada vez mais próximo do [tex] VE=3,5[/tex], quanto mais aumentamos o valor de [tex] n.[/tex]
É só clicar no botão abaixo e conferir!
O que vimos com o exemplo acima é uma consequência da Lei dos Grandes Números; e isso acontecerá com qualquer experimento que seja executado um número muito grande de vezes!
Vejamos porque isso acontece.
Para tanto, consideremos um experimento aleatório [tex]E[/tex] qualquer, cujo espaço amostral [tex]\Omega[/tex] é escrito como união de eventos dois a dois disjuntos
[tex]\qquad \Omega=E_1 \cup E_2 \cup \dots \cup E_k,[/tex]
e, a partir dos números reais [tex]e_1, e_2, \dots, e_k[/tex], consideremos também a associação
[tex]\qquad e_1 \to E_1, \dots, e_k \to E_k.[/tex]
O valor esperado para o experimento [tex]E[/tex], com esta associação, será
[tex]\qquad VE=e_1P(E_1) +e_2P(E_2)+ \dots +e_kP(E_k).[/tex]
Agora, vamos realizar esse experimento aleatório [tex]n[/tex] vezes e considerar a soma [tex]S_n[/tex] cujas parcelas são os números associados aos eventos ocorridos em cada uma das [tex]n[/tex] realizações do experimento.
Se [tex]m_1, m_2, \dots, m_k[/tex] são as quantidades de vezes que ocorreram os eventos [tex]E_1, E_2, \dots, E_k[/tex], respectivamente, então:
[tex]\qquad S_n=m_1e_1+m_2e_2+\dots+m_ke_k.[/tex]
Pela Lei dos Grandes Números, temos as aproximações
[tex]\qquad P(E_1)\approx \dfrac{m_1}{n}, \ \ \ P(E_2)\approx\dfrac{m_2}{n}, \ \ \ \dots, \ \ \ P(E_k)\approx\dfrac{m_k}{n},[/tex]
ou ainda,
[tex]\qquad m_1\approx nP(E_1), \ \ \ m_2\approx nP(E_2), \ \ \ \dots, \ \ \ m_k\approx nP(E_k).[/tex]
Devemos lembrar sempre que estas aproximações serão cada vez melhores à medida que aumentamos o valor de [tex]n[/tex]. Assim,
[tex]\qquad S_n\approx nP(E_1)e_1+nP(E_2)e_2+\dots+nP(E_k)e_k.[/tex]
e, portanto, a média por realização do experimento será
[tex]\qquad \dfrac{S_n}{n}\approx P(E_1)e_1+P(E_2)e_2+\dots +P(E_k)e_k=VE.[/tex]
Dessa forma, à medida que [tex]n[/tex] aumenta, essa variação por realização do experimento se aproximará mais e mais do valor esperado [tex]VE.[/tex]
No caso do Exemplo 2, sobre estimar a área da região [tex]R[/tex], podemos fazer a decomposição do espaço amostral [tex]\Omega[/tex], formado pelos pontos do quadrado unitário, na união dos eventos disjuntos:
[tex]\qquad \Omega=E\cup E^c[/tex],
em que [tex]E=\{\mathrm{pontos \ em \ } R \}[/tex] e [tex]E^c[/tex] é o evento complementar ao evento [tex]E[/tex], ou seja, [tex]E^c=\{\mathrm{pontos \ fora \ de \ R \ }\}[/tex].
Associando ao evento [tex]E[/tex] o número [tex]1[/tex] e ao evento [tex]E^c[/tex] o número [tex]0[/tex], o valor esperado será:
[tex]\qquad VE=1\cdot P(E)+0\cdot P(E^c)=P(E)=\mathrm{Area}(R).[/tex]
Em seguida, usamos o fato que [tex]VE\approx S_n/n[/tex], quando [tex]n[/tex] cresce, e aproximamos [tex]VE=\mathrm{Area}(R)[/tex] por [tex]S_{100}/100=0,35[/tex].
Aplicações
Agora que entendemos o que significa o valor esperado, veremos aplicações nos mais variados assuntos.
Compramos um ticket por [tex]R\$ \ 3,00[/tex] para o lançamento de um dado honesto com faces numeradas de [tex]1[/tex] a [tex]6[/tex] e, em seguida, lançamos o dado e ganhamos, em reais, um valor igual ao número presente na face obtida.
Quanto esperamos ganhar ou perder, em média, por rodada neste jogo?
Solução: Vamos decompor o espaço amostral para o lançamento do dado em eventos disjuntos:
[tex]\qquad \qquad \Omega=\{1\}\cup\{2\} \cup \{3\}\cup \{4\} \cup \{5\} \cup \{6\}.[/tex]
Neste problema, devemos associar os eventos que decompõem o espaço amostral a números que representam nosso ganho ou perda, em reais, a cada vez que este evento ocorre.
- ● Assim, em reais, quando ocorrer o evento [tex]\{1\}[/tex] teremos pago [tex]3[/tex] pelo ticket e recebido [tex]1[/tex] devido ao número da face obtida, ou seja, ganhamos [tex]-2 [/tex].
● De forma análoga, vamos associar [tex]\{2\}[/tex] ao valor [tex]-1[/tex]; [tex]\{3\}[/tex] ao valor [tex]0[/tex]; [tex] \{4\}[/tex] ao valor [tex]1[/tex]; [tex]\{5\}[/tex] ao valor [tex]2[/tex] e [tex]\{6\}[/tex] ao valor [tex] 3[/tex].
O valor esperado será então:
[tex]\qquad VE=-2\cdot\dfrac{1}{6} -1\cdot\dfrac{1}{6}+ 0\cdot\dfrac{1}{6}+1\cdot\dfrac{1}{6}+2\cdot\dfrac{1}{6}+3\cdot\dfrac{1}{6}=\dfrac{3}{6}=0,5.[/tex]
Assim, esperamos ganhar [tex]R\$ \, 0,50[/tex], em média, por rodada neste jogo. Isso significa que, por exemplo, se jogarmos [tex]1.000[/tex] rodadas, ganharemos algo próximo a [tex]R\$ \, 500,00[/tex].
Um jogo lucrativo!
A escola da Rafaela vai realizar uma festa no próximo domingo visando arrecadar fundos para reformar a quadra de esportes. Entre as várias atrações da festa, será disponibilizada uma Roleta Europeia para que as pessoas façam apostas na chamada modalidade dobro-ou-nada. Nessa modalidade o apostador paga uma quantidade [tex]Q[/tex] e deve escolher uma das cores: vermelha ou preta. A roleta então é girada e, se o número sorteado for da mesma cor da escolhida pelo apostador, ele dobra o dinheiro que apostou; se não for da mesma cor, ele perde o dinheiro.
O apostador não pode escolher a cor verde; toda vez que esta cor sair, a escola ficará com as apostas.
Roleta Europeia
 Imagem extraída do site do Freepik.(Acesso em 14/04/2024.)
Imagem extraída do site do Freepik.(Acesso em 14/04/2024.)
(a) Qual é o valor esperado por jogada na modalidade dobro-ou-nada quando alguém apostar um valor de [tex]R\$ \ 10,00[/tex] na cor vermelha?
(b) Quanto a escola vai ganhar por rodada na modalidade dobro-ou-nada quando um apostador apostar [tex]R\$ \ 10,00[/tex] em uma cor?
Solução:
(a) O espaço amostral para o experimento aleatório “girar a roleta e obter um número” é
[tex]\qquad \qquad \Omega=\{0, 1, 2, 3, \dots, 36 \}.[/tex]
Se a roleta for honesta, este espaço amostral é finito e equiprovável.
Vamos considerar o evento [tex]E=\{\mathrm{números \ com \ cor \ vermelha}\}[/tex].
Podemos fazer a decomposição do espaço amostral em:
[tex]\qquad \qquad \Omega=E\cup E^c,[/tex]
com [tex]E^c[/tex] denotando o evento complementar do evento [tex]E[/tex], ou seja, [tex] E^c=\{\mathrm{números \ com \ cor \ não-vermelha}\}[/tex].
- ● Vamos associar ao evento [tex]E[/tex] o valor que alguém ganharia se a roleta parasse na cor vermelha, neste caso, [tex]R\$ \ 10,00[/tex] (ou seja, [tex] R\$ \ 20,00[/tex], menos os [tex]R\$ \ 10,00[/tex] que foi apostado).
● Ao evento [tex]E^c[/tex] vamos associar o valor que alguém ganharia se a roleta parasse em um número com uma cor não-vermelha, ou seja, [tex]R\$ \ -10,00[/tex].
Assim, o valor esperado nesta aposta será
[tex]\quad \quad VE=10\cdot P(E)-10\cdot P(E^c)\\
\quad \quad VE=10\cdot P(E)-10\cdot (1-P(E))\\
\quad \quad VE=20\cdot P(E)-10.[/tex]
Usando a definição clássica de probabilidade, podemos calcular a probabilidade de ocorrer o evento [tex]E:[/tex]
[tex]\quad \quad P(E)=\dfrac{n(E)}{n(\Omega)}=\dfrac{18}{37}.[/tex]
Portanto,
[tex]\quad \quad VE=20\cdot \dfrac{18}{37}-10\\
\quad \quad VE=\dfrac{360-370}{37}\\
\quad \quad VE=-\dfrac{10}{37}\\
\quad \quad VE\approx -0,27.[/tex]
A pessoa perderá aproximadamente [tex]27[/tex] centavos a cada aposta dobro-ou-nada de [tex] R\$ \ 10,00[/tex] na Roleta Europeia. A conclusão a que chegamos é que jogando a Roleta Europeia muitas e muitas vezes uma pessoa irá sempre perder dinheiro.
Bom para a escola!
(b) Primeiramente, vamos fazer a seguinte observação: se um apostador perde aproximadamente [tex]27[/tex] centavos a cada aposta dobro-ou-nada de [tex]R\$ \ 10,00[/tex] na roleta europeia, então é natural que a escola ganhe esses [tex]27[/tex] centavos por rodada, pois o dinheiro não pode simplesmente desaparecer, não é?
Então, vamos tentar chegar a essa conclusão usando a definição de valor esperado, do ponto de vista da escola.
Para isso, consideremos o evento [tex]E=\{\mathrm{números \ com \ a \ cor \ do \ apostador}\}[/tex].
Podemos fazer a decomposição do espaço amostral em
[tex]\qquad \qquad \Omega=E\cup E^c. [/tex]
Vamos associar ao evento [tex]E[/tex] o valor que a escola ganha quando a roleta para na cor escolhida pelo apostador, neste caso, [tex]R\$ \ -10,00[/tex], e ao evento [tex]E^c[/tex] o valor que a escola ganha quando a roleta não para na cor escolhida pelo apostador, ou seja, [tex]R\$ \ 10,00[/tex]. Assim, o valor esperado nesta aposta será:
[tex]\quad \quad VE=-10P(E)+10P(E^c)\\
\quad \quad VE=-10P(E)+10(1-P(E))\\
\quad \quad VE=-20P(E)+10.[/tex]
Assim como no item (a), [tex]P(E)=\dfrac{18}{37}[/tex]; logo,
[tex]\quad \quad VE=-20\cdot \dfrac{18}{37}+10\\
\quad \quad VE=\dfrac{-360+370}{37}\\
\quad \quad VE=\dfrac{10}{37}\\
\quad \quad VE\approx 0,27.[/tex]
- – A cor preta tem quase [tex]50\%[/tex] de chance de aparecer e, portanto, é improvável que fique muitas rodadas tendo apenas as cores vermelha e verde. Vou apostar [tex]R\$ \ 1,00[/tex] na cor preta; se perder, vou apostar [tex]R\$ \ 2,00[/tex] na cor preta; se perder novamente, apostarei [tex]R\$ \ 4,00[/tex] e, assim sucessivamente, sempre dobrando a aposta anterior e sempre apostando na cor preta.
Observe que, quando a cor preta aparecer, ele cobrirá todas as despesas anteriores e ganhará [tex]R\$ \ 1,00[/tex], já que sabemos que:
[tex]\qquad 2^n=(1+2+4+\dots+2^{n-1})+1[/tex].
Esse raciocínio parece muito sólido e seria uma forma fácil de ganhar dinheiro. Entretanto, o apostador em questão não possui recursos ilimitados para continuar dobrando as apostas e pode ficar sem dinheiro para apostar em algum momento.
Suponha, então, que ele tenha levado [tex]R\$ \ 1 \ 023,00[/tex] para apostas e calcule o valor esperado em cada aplicação dessa estratégia.
Solução: Neste problema, veremos como a ideia de valor esperado pode ser útil para se analisar situações mais complexas como a apresentada aqui. Vamos considerar o experimento aleatório “resultado da estratégia do apostador ” que tem espaço amostral [tex] \Omega[/tex] formado pelos resultados [tex]E=\{\mathrm{sucesso}\}[/tex] e [tex]E^c=\{\mathrm{fracasso}\}[/tex]. Observe que o apostador em questão perde todo o seu dinheiro, [tex]1 \ 023[/tex] reais, se não sair a cor preta nas [tex]10[/tex] primeiras rodadas da roleta, já que:
[tex]\quad 1+2+4+8+16+32+64+128+256+512=1023.[/tex]
Então:
[tex]\quad E^c=\{\mathrm{não\ sai \ a \ cor \ preta \ nas \ 10 \ primeiras \ rodadas}\}[/tex].
Observe que a probabilidade de não sair a cor preta em uma rodada é de [tex]\dfrac{19}{37} [/tex] e, como cada giro da roleta é independente um do outro, segue que
[tex]\qquad P(E^c)=\left( \dfrac{19}{37}\right)^{10}.[/tex]
O apostador irá ganhar [tex]1[/tex] real quando ocorrer o evento [tex]E[/tex], ou seja, sair pelo menos uma vez a cor preta nas [tex]10[/tex] primeiras rodadas. Assim:
- ● Vamos associar ao evento [tex]E^c[/tex] o número [tex]\left(-1023\right)[/tex], que é o valor perdido pelo apostador quando ocorre o evento [tex]E^c.[/tex]
● Ao evento [tex]E[/tex] vamos associar o número [tex]1[/tex], o valor ganho pelo apostador na ocorrência deste evento.
Assim, o valor esperado para esta estratégia usada pelo nosso apostador será:
[tex]\quad VE=-1023P(E^c)+P(E)\\
\quad VE=-1023P(E^c)+\left(1-P(E^c)\right)\\
\quad VE=1-1024\left(\dfrac{19}{37}\right)^{10}\\
\quad VE= 1-2^{10}\left(\dfrac{19}{37}\right)^{10}\\
\quad VE=1-\left(\dfrac{38}{37}\right)^{10}\\
\quad VE\approx 1-1,30=-0,30.[/tex]
Pelo exposto, nosso apostador irá perder [tex]30[/tex] centavos, em média, cada vez que aplicar essa estratégia.
Esse método de apostas é conhecido como Método Martingale e é muito usado por apostadores amadores. Ele é ilusório, pois o apostador irá ganhar muitas vezes [tex]1[/tex] real; mas quando perder ele terá um prejuízo de [tex]R\$ \ 1 \ 023,00.[/tex]
Se ele desistir sem tentar respondê-la levará para casa [tex]R\$ \ 500 \ 000,00[/tex]. Por outro lado, se optar por responder e acertar ganhará [tex]R\$ \ 1\ 000 \ 000,00[/tex], mas se errar ganhará apenas [tex]R\$ \ 50 \ 000,00[/tex].
 Imagem extraída do site do Freepik.
Imagem extraída do site do Freepik.
O participante descartou com certeza duas das alternativas disponíveis, mas está igualmente em dúvida sobre as outras duas. Qual é a melhor decisão a ser tomada por este participante, olhando apenas do ponto de vista do valor esperado?
Solução: Primeiramente, devemos observar que nosso participante tem a opção de ir pra casa com [tex]R\$ \ 500 \ 000,00[/tex]. Na outra opção ele iria tentar ganhar o prêmio de [tex]R\$ \ 1\ 000 \ 000,00[/tex]. Vamos calcular o valor esperado para esta opção. Consideremos o evento [tex]E=\{\mathrm{escolher \ a \ alternativa \ correta}\}[/tex]. Como ele está igualmente em dúvida em relação a duas alternativas, podemos dizer que a probabilidade dele ganhar é de [tex]50\%[/tex], sendo esta também a probabilidade dele perder. Assim, [tex]P(E)=0,5[/tex] e [tex]P(E^c)=0,5[/tex]. Vamos associar ao evento [tex]E[/tex] o valor ganho de [tex]R\$ \ 1\ 000 \ 000,00[/tex] e ao evento [tex]E^c[/tex] o valor ganho de [tex]R\$ \ 50 \ 000,00[/tex]. Assim, o valor esperado quando ele arrisca é de
[tex]\qquad VE=0,5 \times 1 \ 000 \ 000 +0,5 \times 50 \ 000=525 \ 000, [/tex]
ou seja, a opção mais lucrativa é arriscar, ”chutando” uma das alternativas. Entretanto, é válido observar que, quando as pessoas têm apenas uma chance, elas preferem escolher a opção segura e levar os [tex]R\$ \ 500 \ 000,00[/tex] para casa. Mas, se elas tivessem a oportunidade de repetir essa escolha muitas vezes, a opção em que elas arriscam é, em média, [tex]R\$ \ 25 \ 000,00[/tex] mais lucrativa.
Wagner, então, decide apostar [tex]R\$ \ 100,00[/tex] na vitória do Time A e seu pai se propõe a pagar [tex]1,6[/tex] reais para cada [tex]1[/tex] real que Wagner apostou, se o time dele vencer a partida, o que fará com que Wagner receba [tex]R\$ \ 160,00[/tex], se ele ganhar a aposta. Caso o time de Wagner não ganhe, os cem reais ficarão com seu pai.
Qual deve ser a probabilidade mínima de vitória do Time A para que a aposta de Wagner apresente valor esperado não negativo?
- Uma moeda honesta será lançada [tex]10[/tex] vezes consecutivas:
– Se não aparecer coroa em todos esses lançamentos o jogador irá ganhar [tex]R\$ \ 1 \ 024,00[/tex].
– Se a primeira coroa que aparecer estiver na posição [tex]i[/tex] da sequência de lançamentos, o cliente ganhará [tex]R\$ \ 2^{i}[/tex]. Por exemplo, se os lançamentos da moeda resultarem em cara, cara, coroa, etc. , o cliente receberá [tex]2^{3}=8[/tex] reais.
Para cobrir as despesas com o oferecimento do jogo, o dono da loja planeja ganhar, em média, [tex]R\$ \ 1[/tex] por cada rodada.
Então qual deve ser o valor cobrado de um apostador para jogá-lo?
A jogada realizada pelo irmão A é lucrativa, ou seja, o valor esperado da sua jogada é positivo?
Um vídeo para ajudar…
Precisa de mais exemplos?
Assista a este vídeo da série Isto é MATEMÁTICA.
Foi dele que retiramos o problema do “Seu João e da Dona Mariazinha”.
É só clicar na telinha!
Enquanto Há Vida, Há Esperança Matemática
Equipe COM – OBMEP
Maio de 2024.
