 |
Apresentaremos aqui algumas definições e propriedades relacionadas aos Coeficientes Binomiais e ao mecanismo numérico conhecido como Triângulo de Pascal, para ajudar na resolução de alguns problemas postados no nosso Blog. |
Triângulo de Pascal e Coeficientes Binomiais
Nesta nossa breve discussão, no número binomial [tex]\dbinom{n}{r}[/tex], denominaremos [tex]n[/tex] de índice superior e [tex]r[/tex] de índice inferior.
- números binomiais que tenham o mesmo índice superior fiquem na mesma linha, ordenados sequencialmente pelos índices inferiores e
- números binomiais que tenham o mesmo índice inferior fiquem na mesma coluna, ordenados sequencialmente pelos índices superiores.
[tex]\textcolor{#800000}{\dbinom{0}{0}\\
\dbinom{1}{0} \dbinom{1}{1}\\
\dbinom{2}{0} \dbinom{2}{1} \dbinom{2}{2}\\
\dbinom{3}{0} \dbinom{3}{1} \dbinom{3}{2}\dbinom{3}{3}\\
\dbinom{4}{0} \dbinom{4}{1} \dbinom{4}{2}\dbinom{4}{3}\dbinom{4}{4}}\\
\qquad \qquad \quad \vdots\\
\textcolor{#800000}{\dbinom{n}{0} \dbinom{n}{1} \dbinom{n}{2}\dbinom{n}{3} \dbinom{n}{4} \cdots \dbinom{n}{n}}\\
\qquad \qquad \quad \vdots\\
[/tex]
Observe que cada linha do Triângulo de Pascal possui uma quantidade finita de elementos, mas as colunas do Triângulo possuem uma quantidade infinita de elementos.
Se for conveniente, podemos escrever o Triângulo de Pascal substituindo cada coeficiente binomial por seu respectivo valor ou até mesmo dispor os números binomiais de forma a obter uma formação diferente do Triângulo.
Veja o Triângulo de Pascal com os coeficientes binomiais que definem as sete primeiras linhas calculados e visualizado nas duas formas mais utilizadas:
|
[tex] |
\begin{equation}\textcolor{#800000}{1 \, \\ 1 \, \quad \, 1 \, \\ 1 \, \quad \, 2 \, \quad \, 1 \, \\ 1 \, \quad \, 3 \, \quad \, 3 \, \quad \, 1 \, \\ 1 \, \quad \, 4 \, \quad \, 6 \, \quad \, 4 \, \quad \, 1 \, \\ 1 \, \quad \, 5 \, \quad \, 10 \, \quad \, 10 \, \quad \, 5 \, \quad \, 1 \, \\ 1 \, \quad \, 6 \, \quad \, 15 \, \quad \, 20 \, \quad \, 15 \, \quad \, 6 \, \quad \, 1 \, \\ 1 \, \quad \, 7 \, \quad \, 21 \, \quad \, 35 \, \quad \, 35 \, \quad \, 21 \, \quad \, 7 \, \quad 1}\\ \vdots \end{equation} |
As soluções de alguns problemas do nosso Blog utilizam propriedades dos coeficientes binomiais que podem ser visualizadas no Triângulo de Pascal. Essas propriedades serão apresentadas e ilustradas nesta Sala de ajuda, sem nos preocuparmos com suas demonstrações.
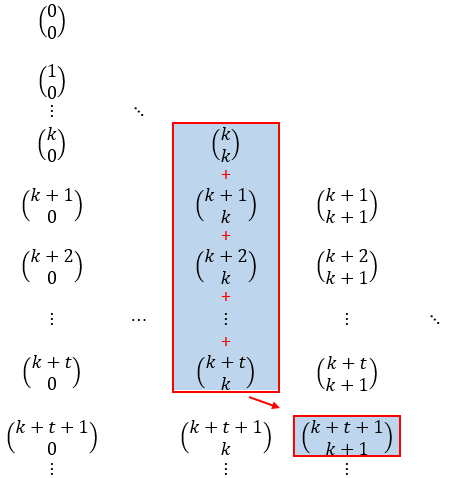
Propriedade 1: Sejam [tex]k[/tex] e [tex]t[/tex] números naturais não nulos. Então:
[tex] \qquad \qquad \begin{pmatrix} k \\ k \end{pmatrix} + \begin{pmatrix} k + 1 \\ k \end{pmatrix} + \begin{pmatrix} k + 2 \\ k \end{pmatrix} + … + \begin{pmatrix} k + t \\ k \end{pmatrix} = \begin{pmatrix} k + t + 1 \\ k + 1 \end{pmatrix} [/tex]
Esta propriedade é conhecida como Teorema das Colunas do Triângulo de Pascal, pois ela pode ser enunciada a partir do Triângulo de Pascal da seguinte forma:
- A soma dos primeiros elementos de uma coluna do Triângulo de Pascal é igual ao elemento que está na linha seguinte e na coluna seguinte da última parcela da soma.(*)
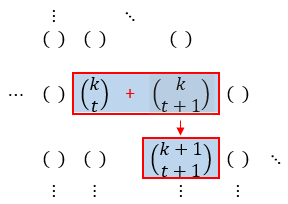
Propriedade 2: Relação de Stifel – Sejam [tex]k[/tex] e [tex]t[/tex] números naturais não nulos. Então:
[tex] \qquad \qquad \begin{pmatrix} k \\ t \end{pmatrix} + \begin{pmatrix} k \\ t+1 \end{pmatrix} = \begin{pmatrix} k+1 \\ t+1 \end{pmatrix} [/tex].
Esta propriedade também pode ser enunciada a partir do Triângulo de Pascal da seguinte forma:
- Somando dois elementos consecutivos de uma mesma linha obtém-se o elemento situado abaixo da segunda parcela.(*)
(*) Tenham em conta que a maneira diferente de escrevermos as Propriedades 1 e 2 não são demonstrações e nem justificativas para elas.
