Funções
Injetividade, sobrejetividade e bijetividade
Até o momento, vocês foram apresentados a cinco definições: função, função entre dois conjuntos, função injetora, função sobrejetora e função bijetora. Vamos relacionar a seguir essas definições, algumas com suas respectivas alternativas de enunciado.
[tex]\qquad f:A \rightarrow B\\
\qquad \quad \, \, x \mapsto y [/tex]
para indicá-la. Neste caso:
➤ o conjunto [tex]A[/tex] é dito o domínio da função [tex]f[/tex];
➤ o conjunto [tex]B[/tex] é dito o contradomínio da função [tex]f[/tex];
➤ o único elemento de [tex]B[/tex] associado a [tex]x[/tex] é denotado por [tex]f(x)[/tex] e é dito a imagem de [tex]x[/tex] pela [tex]f[/tex].
[tex]\qquad \qquad \forall \, x_1,x_2\in A, x_1\ne x_2 \Rightarrow f(x_1) \ne f(x_2)[/tex].
[tex]\qquad \qquad \forall \, x_1,x_2\in A, f(x_1)=f(x_2) \Rightarrow x_1= x_2 [/tex].
[tex]\qquad \qquad \forall \, y\in B, \exists \, x\in A[/tex] tal que [tex]y=f(x)[/tex].
É usual definirmos como imagem da função [tex]f[/tex] o conjunto formado pelos elementos de [tex]B[/tex] que são imagens de algum elemento de [tex]A[/tex]. Esse conjunto é indicado por [tex]Im(f)[/tex]; assim:
[tex]\qquad \qquad Im(f)=\{f(x)\text{ tais que } x\in A \}[/tex].
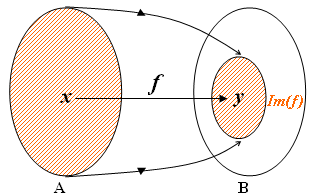
A partir dessa definição podemos dizer que uma função [tex] f:A \rightarrow B [/tex] é sobrejetora se [tex]Im(f)=B[/tex].
Para ajudar na compreensão e no amadurecimento dos conceitos acima, apresentamos três vídeos.
O segundo e o terceiro vídeos trazem lá no finalzinho uma aplicação surpreendente de bijeção!
Bons estudos!
Funções
Vídeo disponibilizado pelo PROFMAT
Funções
Aula ministrada pelo professor Elon Lages Lima, um dos maiores matemáticos do Brasil.
O professor Elon faleceu recentemente; neste vídeo ele tinha 85 anos!
Números Cardinais e Funções Naturais
Aula ministrada pelo professor Eduardo Wagner, um primor de expositor!
Quem já foi a algum [tex]EH^2[/tex] com certeza vai se lembrar dele…
 |
Vocês se lembram do comentário que fizemos lá na sala sobre fórmulas proposicionais? |
Equipe COM – OBMEP
