Funções
Funções invertíveis (2)
O objeto central desta nossa discussão é a definição de função invertível. Nada de novo vai aparecer por aqui, vamos apenas fazer uma compilação das definições e das propriedades importantes sobre o assunto.
Seja [tex]f: A \rightarrow B [/tex] uma função.
A função [tex]f[/tex] é dita invertível se existir uma função [tex]g[/tex] de [tex]B[/tex] em [tex]A[/tex] tal que:
[tex]\qquad \left( g\circ f\right)(x)=x [/tex], para todo [tex]x \in A[/tex];
[tex]\qquad \left( f\circ g\right)(x)=x [/tex], para todo [tex]x \in B[/tex].
Neste caso, é possível provar que a função [tex]g[/tex] é única; então ela é dita a inversa de [tex]f[/tex] e é denotada por [tex]f^{-1}[/tex].
No módulo anterior e no texto do professor Elon foi observado e mostrado que existe uma condição necessária e suficiente para que uma função seja invertível.
Uma função é invertível se, e somente se, for uma bijeção.
Lembre-se sempre de que:
✐ A não injetividade de uma função não permite que a cada elemento do domínio da possível inversa seja associada apenas uma imagem.
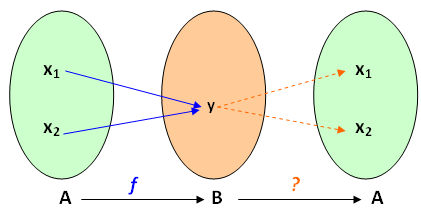
✐ A não sobrejetividade de uma função não permite que todo elemento do domínio da possível inversa tenha imagem.
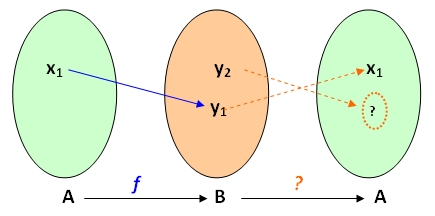
Clique no botão abaixo e veja ilustrações dessas duas observações.
Não se esqueça de fechar a janelinha após o término do vídeo!
Embora nossa proposta não seja trabalhar com exemplos de funções e sim com conceitos, uma observação importante no que tange às funções de [tex]A[/tex] em [tex]B[/tex], com [tex]A,B \, \subset \mathbb{R}[/tex], é que os gráficos de uma função invertível e da sua inversa têm uma característica geométrica interessante; veja:
Seja [tex]f:A \rightarrow B[/tex] uma função invertível.
Se [tex]A, \, B[/tex] forem subconjuntos de [tex]\mathbb{R}[/tex], então os gráficos da [tex]f[/tex] e da [tex]f^{-1}[/tex] são simétricos com relação a reta definida por [tex]y=x[/tex].
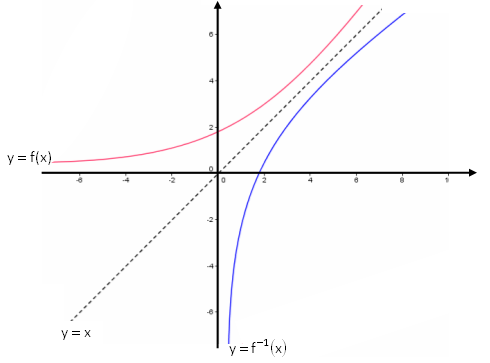
Traduzindo em miúdos, “se você desenhar os dois gráficos em uma folha de papel e dobrar essa folha segundo a reta [tex]y=x[/tex] (diagonal principal do sistema cartesiano utilizado) os dois gráficos coincidirão.”
Clique no botão abaixo para ver uma vez mais a definição de função invertível, mais alguns exemplos e uma abordagem sobre essa simetria entre os gráficos de uma função invertível e de sua inversa.
Não se esqueça de fechar a janelinha após o término do vídeo!
Quando uma função [tex]f[/tex] é invertível, a sua inversa [tex]f^{-1}[/tex] é também uma função, obviamente. Assim, para subconjuntos do domínio e do contradomínio da [tex]f^{-1}[/tex] é possível calcularmos, respectivamente, imagens diretas e imagens inversas.
Algumas observações a esse respeito.
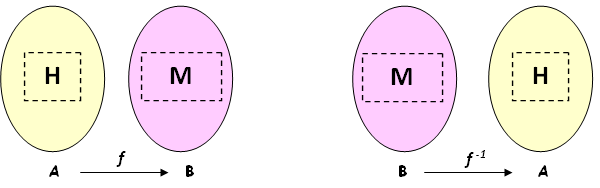
Sejam [tex]f: \, A \rightarrow B[/tex] uma função invertível e [tex]f^{-1}: \, B \rightarrow A[/tex] a sua inversa. Considere conjuntos [tex]H[/tex] e [tex]M[/tex] tais que [tex]H \subset A [/tex] e [tex]M \subset B [/tex].
Assim:
(1) Se [tex]M[/tex] é a imagem direta de [tex]H[/tex] pela [tex]f[/tex], então [tex]M[/tex] é a imagem inversa de [tex]H[/tex] pela [tex]f^{-1}[/tex]. Em símbolos:
[tex]\qquad \qquad M=f\left(H \right) \, \Rightarrow M=\left(f^{-1}\right)^{-1}\left(H \right)[/tex]
(2) Se [tex]H[/tex] é a imagem inversa de [tex]M[/tex] pela [tex]f[/tex], então [tex]H[/tex] é a imagem direta de [tex]M[/tex] pela [tex]f^{-1}[/tex]. Em símbolos:
[tex]\qquad \qquad H=f^{-1}\left(M \right) \, \Rightarrow H=\left(f^{-1}\right)\left(M\right)[/tex]
(3) Se [tex]H[/tex] é a imagem direta de [tex]M[/tex] pela [tex]f^{-1}[/tex], então [tex]H[/tex] é a imagem inversa de [tex]M[/tex] pela [tex]f[/tex]. Em símbolos:
[tex]\qquad \qquad H=\left(f^{-1} \right)\left(M \right) \, \Rightarrow H=f^{-1}\left(M \right)[/tex]
(4) Se [tex]M[/tex] é a imagem inversa de [tex]H[/tex] pela [tex]f^{-1}[/tex], então [tex]M[/tex] é a imagem direta de [tex]H[/tex] pela [tex]f[/tex]. Em símbolos:
[tex]\qquad \qquad M=\left(f^{-1}\right)^{-1}\left(H \right) \, \Rightarrow M=f\left(H \right)[/tex]
Portanto, por (1) e (4)
[tex]\qquad \qquad M=f\left(H \right) \, \Leftrightarrow M=\left(f^{-1}\right)^{-1}\left(H \right)[/tex];
e por (2) e (3)
[tex]\qquad \qquad H=f^{-1}\left(M \right) \, \Leftrightarrow H=\left(f^{-1}\right)\left(M\right)[/tex].
A partir das observações anteriores, se tomamos, particularmente, [tex]H=A[/tex] e [tex]M=B[/tex], então obtemos mais duas relações interessantes.
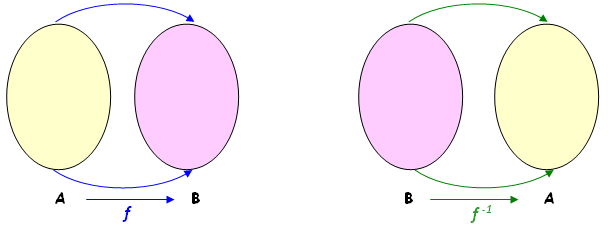
Sejam [tex]f: \, A \rightarrow B[/tex] uma função invertível e [tex]f^{-1}: \, B \rightarrow A[/tex] a sua inversa. Então:
(1) O conjunto imagem da função [tex]f[/tex] é a imagem inversa de [tex]A[/tex] pela função [tex]f^{-1}[/tex]:
[tex] \qquad Im(f)=f\left(A \right)=B=\left(f^{-1}\right)^{-1}\left(A \right)[/tex].
(2) O conjunto imagem da função [tex]f^{-1}[/tex] é a imagem inversa de [tex]B[/tex] pela função [tex]f[/tex]:
[tex]\qquad Im(f^{-1})=\left(f^{-1}\right)\left(B \right)=A=f^{-1}\left(B \right)[/tex].
Uma pequena sutileza é perceber que, como a inversa de uma função invertível é única, então podemos calcular essa inversa. Assim, se [tex]f:A \rightarrow B[/tex] é uma função invertível, então o domínio e o contradomínio da inversa já estão definidos, pois [tex]f^{-1}: \, B \rightarrow A[/tex]. Para determinar a regra [tex]y=f^{-1}(x)[/tex], basta utilizar a relação [tex]a=f^{-1}(b)\Leftrightarrow b=f(a)[/tex] e fazer continhas…
(Passo 0: Verificar se [tex]f[/tex] é uma bijeção)
Passo 1: Escreva [tex]y = f(x)[/tex].
Passo 2: Isole [tex]x[/tex] na equação [tex]y = f(x)[/tex], escrevendo-o em termos de [tex]y[/tex].
Passo 3: Escreva [tex]x = f^{-1}(y)[/tex].
Passo 4: Se quiser expressar a inversa [tex] f^{-1}[/tex] em função de [tex]x[/tex], troque [tex]x[/tex] por [tex]y[/tex] na igualdade obtida no passo 3 e escreva [tex]y = f^{-1}(x)[/tex].
Importante: Não se esqueça de explicitar o domínio e o domínio da inversa.
Precisa de exemplos?
Assista aos próximos vídeos!
Não se esqueça de fechar a respectiva janelinha após o término de cada vídeo!
Exercícios
Para você se exercitar, vamos deixar aqui quatro vídeos com exercícios resolvidos envolvendo injetividade e sobrejetividade e uma lista extraída do volume 1 da coleção Fundamentos de Matemática Elementar contendo exercícios sobre funções invertíveis (muitos com resposta e alguns até com solução).
Vídeos
Não se esqueça de fechar a respectiva janelinha após o término de cada vídeo!
Lista de exercícios…
Para copiar o material, clique no botão abaixo.
Bons estudos!
Equipe COM – OBMEP
