.Probleminha: Volume do cubo

Problema
(Indicado a partir do 9º ano do E. F.)

Solução

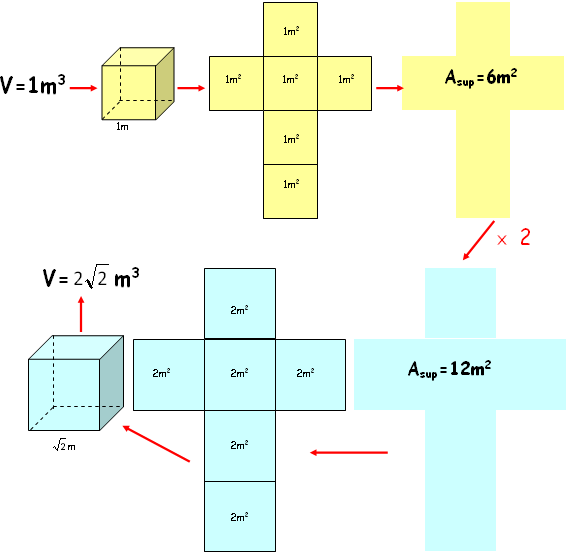
• Um cubo com volume $1 \ m^3$ possui lado de comprimento $\sqrt[3]{1}=1 \ m$ e, assim, a área da superfície desse cubo será $6 \cdot 1^2=6 \ m^2$. Com isso, o dobro da área da sua superfície é $6\cdot2=12 \ m^2$, que sabemos ser a área da superfície do outro cubo em questão.
• Como a área da superfície do segundo cubo é $12 \ m^2$, então a área de cada face deste outro cubo será $\frac{12}{6}=2 \ m^2$, ou seja, o segundo cubo possuirá lado de comprimento $\sqrt{\frac{12}{6}}=\sqrt{2} \ m$ e, portanto, seu volume será dado por $(\sqrt{2})^3=2\sqrt{2} \ m^3$.

Solução elaborada pelos Moderadores do Blog.