Problema
(Indicado a partir do 9º ano do E. F.)
Suponhamos que seja possível colocar uma corda circundando a Terra, ajustando-a ao Equador. Em seguida, retiramos esta corda, aumentamos um metro no seu comprimento e a recolocamos em volta da Terra, formando uma circunferência concêntrica com o Equador.
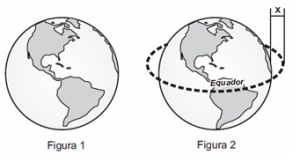
Assim, teremos um vão entre o Equador e a corda, ou melhor, uma diferença [tex]x[/tex] entre os raios das duas circunferências.
Qual o valor de [tex]x[/tex]?
Solução
O comprimento da circunferência da Terra, ou seja, o comprimento da corda original, é [tex]C=2\pi R[/tex], sendo [tex]R[/tex] a medida do raio da Terra. Neste problema, particularmente, consideraremos a medida do raio [tex]R[/tex] em metros.
Observe que, aumentando em [tex]1[/tex] metro o comprimento da corda, o raio aumenta [tex]x[/tex] metros e, assim:
- [tex]C+1=2\pi(R+x)[/tex].
Mas,
[tex]\qquad C+1=2\pi(R+x) \Leftrightarrow C+1=2\pi R+2\pi x \Leftrightarrow C+1=C+2\pi x[/tex],
donde [tex] x=\dfrac{1}{2\pi}[/tex] m.
Portanto, [tex] x \approx 0,15915[/tex] m, ou seja, aproximadamente [tex]16[/tex] cm!
Solução elaborada pelo COM Parentesco Genial, com contribuições dos Moderadores do Blog.
Participou da discussão o COM Parentesco Genial.
