Problema
(Indicado a partir do 8º ano do E. F.)
Francimar recortou três triângulos com tamanhos distintos de uma cartolina branca. Em seguida formou a figura mostrada abaixo, na qual os pontos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] estão alinhados.
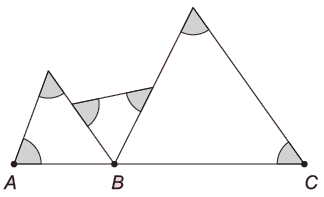
Com um lápis de cor cinza, ele destacou os seis ângulos mostrados na figura. Qual a soma das medidas desses seis ângulos?
Solução 1
- A soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex]. Logo, a soma das medidas dos ângulos internos de todos os triângulos que Francimar recortou é [tex]\boxed{180^\circ \times 3}.[/tex]
- Observe que as medidas dos três ângulos não marcados dos triângulos (com vértices em [tex]B[/tex]) somam [tex]\boxed{180^\circ}[/tex], já que os pontos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex] estão alinhados.
Assim, a soma dos ângulos marcados é [tex]\boxed{180^\circ \times 3}-\boxed{180^\circ}= \, \fcolorbox{black}{#eee0e5}{$ \, 360^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Para resolver este problema, precisamos primeiro saber duas informações: a soma total dos ângulos internos dos triângulos e o valor dos três ângulos que não estão em cinza.
Sabe-se que a soma dos três ângulos internos de um triângulo é sempre igual a [tex]180^\circ[/tex]. Sendo assim, se temos 3 triângulos, apenas precisamos somar 3 parcelas iguais a [tex]180^\circ[/tex] que nos dará o valor de [tex]540^\circ (180^\circ \times 3 = 540^\circ)[/tex].
Agora que já descobrimos qual o valor total da soma de todos os ângulos internos, vamos para a segunda informação. Sabemos que um círculo possui [tex]360^\circ[/tex] e se cortarmos o círculo ao meio teremos duas metades de [tex]180^\circ[/tex].
No enunciado da questão foi dito que os pontos [tex]A, B[/tex] e [tex]C[/tex] estão alinhados, sendo que [tex]B[/tex] está no meio. Se desenhássemos um círculo em volta de [tex]B[/tex], ele cortaria o círculo ao meio. Sendo assim, a soma dos ângulos dos triângulos que não estão pintados de cinza tem o valor de [tex]180^\circ[/tex].
Para sabermos agora qual o valor da soma dos ângulos pintados em cinza, só precisaremos tomar os [tex]540^\circ[/tex] descobertos anteriormente e deles subtrair [tex]180^\circ[/tex]. Então teremos [tex]540^\circ – 180^\circ = 360^\circ[/tex].
Solução elaborada pelo COM Classe S, com contribuições dos Moderadores do Blog