✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 8º ano do E. F.)
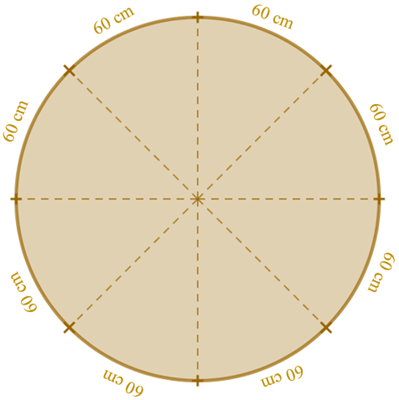
(EsPCEx, 2021 – Adaptado) Para fabricar uma mesa redonda que comporte oito pessoas em sua volta, um projetista concluiu que essa mesa, para ser confortável, deverá considerar, para cada um dos ocupantes, um arco de circunferência com no mínimo [tex]60\text{ cm}[/tex] de comprimento.
O tampo redondo da mesa será obtido a partir de uma placa quadrada de madeira compensada.

Adotando [tex]\pi = 3,14[/tex], qual a menor medida, em centímetros, do lado dessa placa quadrada que permite obter esse tampo de mesa?
Solução
Como para cada um dos ocupantes será considerado um arco de circunferência com no mínimo [tex]60\text{ cm}[/tex], então o comprimento total da circunferência que representa o contorno do tampo da mesa será de no mínimo [tex]8\times 60 = 480 \text{ cm}[/tex].
Por outro lado, sabemos que o comprimento de uma circunferência de raio [tex]r[/tex] é dado por [tex]2\cdot \pi\cdot r[/tex]. Assim, segue que:
[tex]\qquad 2\cdot \pi\cdot r = 480\\
\qquad 2r = \dfrac{480}{3,14} \approx 152,87.[/tex]
Como vimos na figura do enunciado, a placa quadrada que dará origem ao tampo da mesa tem medida do lado igual ao diâmetro da mesma, ou seja, [tex]2r[/tex].
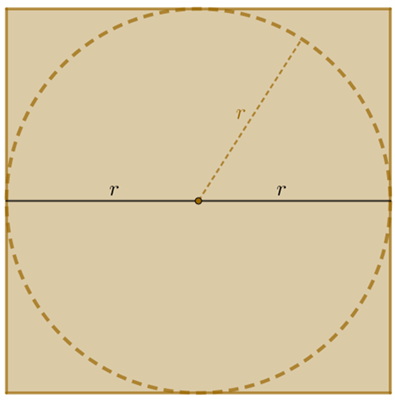
Logo, a menor medida do lado dessa placa quadrada é, aproximadamente, [tex]\fcolorbox{black}{#eee0e5}{$152,87\text{ cm}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
