Problema
(Indicado a partir do 9º ano do E. F.)
Qual a soma dos algarismos do número que se obtém elevando ao quadrado [tex]\boxed{\,5\underbrace{00\dots0}_{2019 \, zeros}1\,} \, [/tex]?
(Problema adaptado das Olimpíadas Portuguesas de Matemática)
Solução
Seja [tex] N = 5\underbrace{00\dots0}_{2019 \, zeros}1[/tex] e observe que esse número pode ser representado por [tex] \boxed{\,N = 5 \cdot 10^{2020} + 1\,} \, .[/tex]
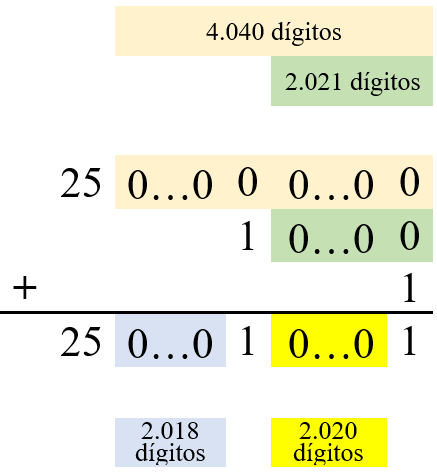
Portanto, segue que:
[tex]\qquad N^2=(5\cdot10^{2020} + 1)^2\\
\qquad N^2=25\cdot10^{4040} + 10\cdot10^{2020} + 1\\
\qquad N^2=25\cdot10^{4040} + 10^{2021} + 1\\
\qquad N^2=25\underbrace{00\dots0}_{4040 \, zeros} + 1\underbrace{00\dots0}_{2021 \, zeros} + 1[/tex]
ou ainda,
[tex] \qquad \boxed{\,N^2 = 25\underbrace{00\dots0}_{2018 \, zeros}1\underbrace{00\dots0}_{2020 \, zeros}1 \,}[/tex], cuja soma dos algarismos é [tex] 9 [/tex].
Solução elaborada pelos Moderadores do Blog.
