Problema
(Indicado a partir do 8º ano do E. F.)
Observe a reta numérica:

Nela, o segmento [tex]\overline{XY}[/tex] foi dividido em dez segmentos congruentes determinados pelos pontos assinalados pelas letras [tex]A[/tex], [tex]B[/tex], [tex]C[/tex], [tex]D[/tex],[tex]E[/tex],[tex]F[/tex], [tex]G[/tex], [tex]H[/tex], [tex]I[/tex].
Considerando que os pontos [tex]X[/tex] e [tex]Y[/tex] representem, respectivamente, [tex]\dfrac{1}{5} \, [/tex] e [tex] \, \dfrac{5}{9}[/tex], determine a qual número a letra [tex]E[/tex] corresponde.
Notação: Se [tex]R \, [/tex] e [tex] \, S[/tex] são pontos quaisquer, consideramos que [tex]\overline{RS}[/tex] representa o segmento e [tex]RS[/tex] representa a medida desse segmento.
Solução
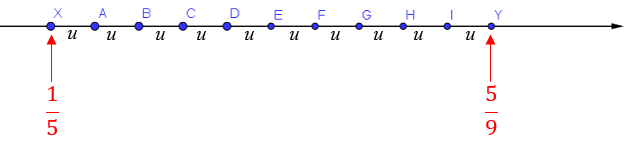
Sendo [tex]u[/tex] o comprimento dos dez segmentos em questão, isto é, [tex]XA=AB=BC=\cdots=IY=u[/tex], temos:
[tex]\qquad \qquad \dfrac{5}{9}=\dfrac{1}{5}+10u[/tex]
[tex]\qquad \qquad \dfrac{5}{9}-\dfrac{1}{5}=10u[/tex]
[tex]\qquad \qquad \dfrac{25-9}{45}=10u[/tex]
[tex]\qquad \qquad \dfrac{16}{45}=10u[/tex]
[tex]\qquad \qquad \dfrac{16}{45\times 10}=u[/tex]
[tex]\qquad \qquad \dfrac{8}{225}=u \, .[/tex]
Dessa forma, se [tex]x[/tex] é o número real que corresponde ao ponto [tex]E[/tex], então:
[tex]\qquad \qquad x=\dfrac{1}{5} + 5u[/tex]
[tex]\qquad \qquad x=\dfrac{1}{5} + 5\times\dfrac{8}{225}[/tex]
[tex]\qquad \qquad x=\dfrac{1}{5} + \dfrac{8}{45}[/tex]
[tex]\qquad \qquad x= \dfrac{9+8}{45}[/tex]
[tex]\qquad \qquad x= \dfrac{17}{45}.[/tex]
Portanto, o ponto representado pela letra [tex]E[/tex] corresponde ao número [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{17}{45}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
