Problema
(Indicado a partir do 9º ano do E. F.)
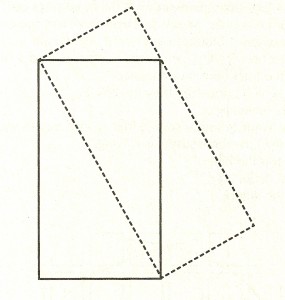
O retângulo vertical (linha contínua) tem uma área de 40 cm².
Sendo assim, qual a área do retângulo inclinado (linha pontilhada)?
Solução 1
Considere a figura a seguir.
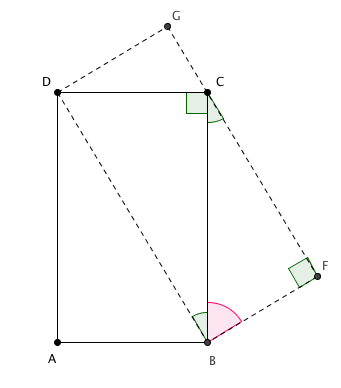
Perceba que os ângulos [tex]D\hat{B}C[/tex] e [tex]B\hat{C}F[/tex] são congruentes, pois ambos são complemento de [tex]C\hat{B}F[/tex]. Deste modo, os triângulos [tex]BCD[/tex] e [tex]CFB[/tex] são semelhantes, já que possuem dois ângulos ordenadamente congruentes e, por conseguinte, temos os lados destes triângulos proporcionais.
Assim, segue que:
[tex]\qquad \dfrac{BD}{BC} = \dfrac{CD}{BF}\\
\qquad BD \cdot BF = CD \cdot BC \\
\qquad \boxed{BD \cdot BF = 40}.[/tex]
Logo, o retângulo “inclinado” tem área de [tex]40\,cm^2[/tex].
Solução enviada pelo Clube Os Modulares, com contribuições dos Moderadores.
Solução 2
Considere a figura do problema na qual renomeamos os vértices e traçamos o segmento [tex]\overline{BG}[/tex] perpendicular ao segmento [tex]\overline{AC}[/tex]. Além disso, [tex]A_1[/tex], [tex]A_2[/tex], [tex]A_3[/tex], [tex]A_4[/tex] e [tex]A_5[/tex] indicam as áreas dos respectivos triângulos retângulos.
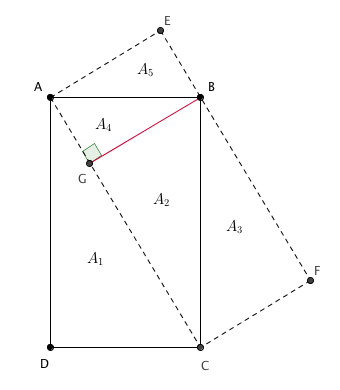
A diagonal de um retângulo divide-o em dois triângulos congruentes e, portanto, de mesma área. Deste modo, temos:
[tex]\quad \textcolor{#800000}{(i)} \,\,A_2 = A_3[/tex];
[tex]\quad \,\textcolor{#800000}{(ii)}\,\,A_4 = A_5[/tex];
[tex]\quad \,\textcolor{#800000}{(iii)}\,\,A_1 = A_2 + A_4[/tex].
De [tex]\textcolor{#800000}{(iii)}[/tex], temos que [tex]A_2 + A_4[/tex] é metade da área do retângulo vertical.
Por outro lado, somando membro a membro as equações [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], temos [tex]A_2 + A_4 = A_3 + A_5[/tex], ou seja, [tex]A_2 + A_4[/tex] também é metade da área do retângulo inclinado.
Concluímos, assim, que os dois retângulos possuem mesma área e, portanto, a área do retângulo inclinado é [tex]40\,cm^2[/tex].
Solução elaborada pelos Moderadores do Blog.
Um applet para ilustrar
Você pode utilizar o applet abaixo para reforçar e explicitar o que os cálculos efetuados comprovam:
- o fato de o retângulo inclinado ter a mesma área do retângulo vertical não é uma particularidade da área medir[tex]40\,cm^2[/tex] e sim da posição em que os retângulos foram construídos.
Na janela inicial do aplicativo, apresentamos a situação discutida no problema, a partir de um retângulo vertical com lados medindo [tex]5\,cm[/tex] e [tex]8\,cm[/tex]. Mas você pode movimentar os pontos vermelhos [tex]\textcolor{red}{B}[/tex] e [tex]\textcolor{red}{D}[/tex] para obter outros retângulos.
A cada movimento, o aplicativo mostrará imediatamente o valor das áreas dos dois retângulos: o retângulo [tex]\textcolor{red}{ABCD}[/tex] e o retângulo [tex]\textcolor{blue}{BFGD}[/tex]. É importante você lembrar que o GeoGebra fornece valores aproximados para as medidas apresentadas.
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para movimentar os pontos [tex]\textcolor{red}{B}[/tex] ou [tex]\textcolor{red}{D}[/tex], clique sobre cada um deles com o botão esquerdo do mouse, mantenha o botão pressionado e faça o movimento lentamente. (Se você estiver utilizando um celular ou um tablet, toque levemente no ponto [tex]\color{red}{B}[/tex] (ou [tex]\color{red}{D}[/tex]) e movimente-o.)
(3) Você poderá fazer movimentos “mais finos” do ponto [tex]\textcolor{red}{B}[/tex] utilizando seu teclado. Para isso, clique sobre o ponto com o botão esquerdo do mouse. Em seguida, mantenha a tecla Shift do teclado apertada e faça os movimentos utilizando as teclas “mover para direita” ou “mover para esquerda”.
(4) Você poderá fazer movimentos “mais finos” do ponto [tex]\textcolor{red}{D}[/tex] utilizando seu teclado. Para isso, clique sobre o ponto com o botão esquerdo do mouse. Em seguida, mantenha a tecla Shift do teclado apertada e faça os movimentos utilizando as teclas “mover para cima” ou “mover para baixo”.
(5) Para voltar para a configuração inicial, é só clicar nas setinhas circulares que aparecem no canto superior direito do applet.
OBMEP_ srdg, criado com o GeoGebra
Observamos que o applet ajuda na visualização do resultado; mas, matematicamente, não substitui sua demonstração.
