Problema
(Indicado a partir do 9º ano do E. F.)
Uma pessoa que nasceu entre os anos 1700 e 1799 completou [tex]N[/tex] anos no ano [tex]N^3[/tex].
Quantos anos ela completou em 1800?
Solução 1
Seja [tex]A[/tex] o ano de nascimento da pessoa em questão, logo [tex]\boxed{1700 \lt A \lt 1799}[/tex].
Mas se essa pessoa completou [tex]N[/tex] anos no ano [tex]N^3[/tex], então [tex]A+N=N^3[/tex], ou seja, ela nasceu no ano [tex]\boxed{A=N^3-N}[/tex].
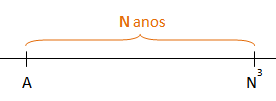
Assim, [tex]N^3-N[/tex] é um número entre [tex]1700[/tex] e [tex]1799[/tex].
Observe que:
- [tex]11^3-11=1320\lt 1700[/tex],
- [tex]13^3-13=2184 \gt 1799[/tex],
logo [tex]N\ne 11[/tex] e [tex]N\ne 13[/tex] e, assim, a única possibilidade é [tex]N=12[/tex].
Neste caso, temos
[tex]\qquad \qquad A=12^3-12=1716[/tex]
e, então, no ano 1800 a pessoa completou [tex]1800-1716=84[/tex] anos.
Solução elaborada pelos Moderadores do Blog.
Solução 2
Sabemos que [tex]10^3 = 1000[/tex], logo [tex]N[/tex] é um número maior e não muito longe de [tex]10[/tex]. Fazendo os testes a seguir podemos perceber que [tex]12[/tex] é a única opção para [tex]N[/tex]:
- [tex]11^3 = 1331[/tex], sendo assim esta pessoa nasceria em [tex]1331 – 11 = 1320[/tex], antes do período pedido pela questão ([tex]1700[/tex] – [tex]1799[/tex]);
- [tex]12^3 = 1728[/tex], desse modo esta pessoa nasceria em [tex]1728 – 12 = 1716[/tex], correspondendo ao período pedido;
- [tex]13^3 = 2197[/tex], logo esta pessoa nasceria em [tex]2197 – 13 = 2184[/tex], ultrapassando o período pedido.
Como esta pessoa completou [tex]N[/tex] anos no ano [tex]N^3[/tex], podemos concluir que ela completou [tex]12[/tex] anos no ano [tex]12^3 = 1728[/tex].
Com esta informação podemos chegar ao seu ano de nascimento: se ela completou [tex]12[/tex] anos em [tex]1728[/tex], logo ela nasceu no ano de [tex]1728 – 12 = 1716[/tex].
Sendo assim, em [tex]1800[/tex] ela completou [tex]1800 – 1716 = 84[/tex] anos.
Solução elaborada pelo COM 1uik.
