Problema
(Indicado a partir do 9º ano do E. F.)
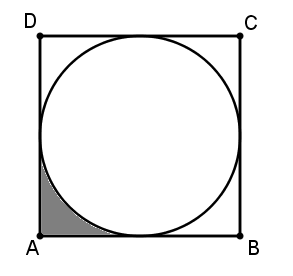
Determine o raio da circunferência inscrita no quadrado ABCD abaixo, sabendo que a área da região sombreada é [tex]2 ~cm^2[/tex].
Solução
Sendo [tex]r[/tex] o raio da circunferência, a área da região sombreada é dada por
[tex]\qquad A = \dfrac{\text{área do quadrado} – \text{área do círculo}}{4}[/tex]
[tex]\qquad A = \dfrac{(2r)^2 – \pi r^2}{4}[/tex]
[tex]\qquad A = \dfrac{4r^2 – \pi r^2}{4}.[/tex]
Por outro lado, temos [tex]A = 2 ~cm^2[/tex].
Assim,
[tex]\qquad \dfrac{4r^2 – \pi r^2}{4} = 2[/tex]
[tex]\qquad 4r^2 – \pi r^2 = 8[/tex]
[tex]\qquad r^2(4 – \pi) = 8[/tex]
[tex]\qquad r^2 = \dfrac{8}{4 – \pi}[/tex]
[tex]\qquad r = \dfrac{2\sqrt{2}}{\sqrt{4 – \pi}}[/tex]
[tex]\qquad r = \dfrac{2\sqrt{2}\cdot \sqrt{4 – \pi}}{\sqrt{4 – \pi}\cdot \sqrt{4 – \pi}}[/tex]
[tex]\qquad r = \dfrac{2 \sqrt{8 – 2\pi}}{4 – \pi}.[/tex]
Portanto, o raio da circunferência é de [tex]r = \dfrac{2 \sqrt{8 – 2\pi}}{4 – \pi} ~cm.[/tex]
Solução elaborada pelos Moderadores do Blog.
