Problema
(Indicado a partir do 9º ano do E. F.)
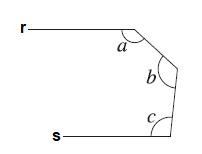
(Cayley Olympiad, 2012) Na figura abaixo, as retas [tex]r[/tex] e [tex]s[/tex] são paralelas.
Determinar a soma [tex]a+b+c[/tex].
Solução
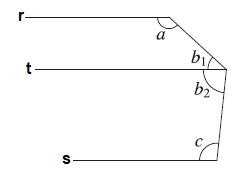
Inicialmente, tracemos a reta [tex]t[/tex] paralela às duas retas já existentes de forma que ela passe pelo vértice do ângulo cuja medida é [tex]b[/tex], conforme indica a figura abaixo.
Observe que a reta [tex]t[/tex] divide o ângulo [tex]b[/tex] em dois outros ângulos, cujas medidas indicaremos por [tex]b_1[/tex] e [tex]b_2[/tex].
Perceba que:
- Os ângulos com medidas [tex]a[/tex] e [tex]b_1[/tex] são colaterais internos; como [tex]t//r[/tex], temos que [tex]a+b_1=180^\circ[/tex], de onde segue que: [tex]\qquad b_1=180^\circ -a \qquad \textcolor{#800000}{(i)}[/tex].
- Analogamente, os ângulos com medidas [tex]c[/tex] e [tex]b_2[/tex] são colaterais internos e [tex]c+b_2=180^\circ[/tex], já que [tex]t//s[/tex]. Assim: [tex]\qquad b_2=180^\circ-c \qquad \textcolor{#800000}{(ii)}[/tex].
Acontece que [tex]b=b_1+b_2[/tex]; logo, substituindo [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex] nessa igualdade, obtemos:
[tex]\qquad b=180^\circ -a + 180^\circ -c\\
\qquad \,\fcolorbox{black}{#eee0e5}{$a+b+c=360^\circ$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
