Problema
(A partir do 7º ano do E. F. – Nível de dificuldade: Médio)
A pintura de quatro triângulos foi feita em uma tela quadrada dividida em quadrinhos [tex]1 \times 1[/tex], conforme mostrado abaixo.
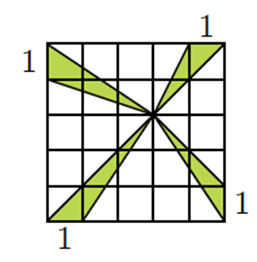
Qual a razão entre a área da tela e a área total dos quatro triângulos?
Solução
Sabemos que se [tex]b[/tex] é a medida de uma das três bases de um triângulo e [tex]h[/tex] a medida da altura relativa a esta base, então a área desse triângulo é dada por [tex]A = \dfrac{b\times h}{2}[/tex].
Como cada altura de um triângulo é um segmento perpendicular à reta que contém a respectiva base, as melhores escolhas para as alturas dos triângulos [tex]T_1, \, T_2, \, T_3, \, T_4[/tex] são as indicadas na próxima figura.
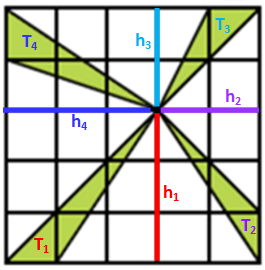
Assim, para [tex]i=1, \, 2, \, 3, \, 4[/tex], se [tex]A_i[/tex] é a respectiva área do triângulo [tex]T_i[/tex], então [tex]A_i=\dfrac{1 \times h_i}{2}=\dfrac{h_i}{2}[/tex], já que as quatro bases são unitárias. Dessa forma, a área total dos quatro triângulos é dada por:
[tex]\qquad A_{total}=A_1+A_2+A_3+A_4=\dfrac{h_1+h_2+h_3+h_4}{2}[/tex]
[tex]\qquad A_{total}=\dfrac{3+2+2+3}{2}=5[/tex] unidades de área.
Por outro lado, a tela é formada por vinte e cinco quadradinhos de área [tex]1[/tex]; assim, sua área é:
[tex]\qquad \quad A_{tela}=25[/tex] unidades de área,
e, portanto, a razão solicitada é dada por:
[tex]\qquad \quad \dfrac{A_{tela}}{A_{total}}=\dfrac{25}{5}=5[/tex].
Solução elaborada pelos Moderadores do Blog.
