Problema
(Indicado a partir do 8º ano do E. F.)
O filho de Maria nasceu no dia em que ela completou [tex]20[/tex] anos. Se hoje a soma das idades de Maria e seu filho é [tex]56[/tex] anos, quantos anos Maria tem?
Solução 1
Se hoje o filho de Maria tiver [tex]\boxed{x}[/tex] anos então Maria terá [tex]\boxed{x+20}[/tex] anos.

Como a soma dessas duas idades deve ser [tex]56[/tex] anos, então segue que:
[tex]\qquad x+(x+20)=56[/tex]
[tex]\qquad 2x=36 \, .[/tex]
[tex]\qquad x=18[/tex].
Logo, Maria tem hoje [tex] \, \fcolorbox{black}{#eee0e5}{$x+20=18+20=38$}[/tex] anos.
Solução elaborada pelos Moderadores do Blog.
Solução 2
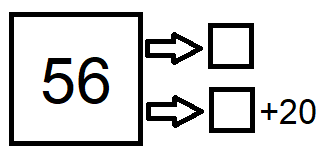
- Como a soma das duas idades é [tex]56[/tex], desenhe um quadrado e dentro dele coloque o [tex]56[/tex].
- Agora, representamos a idade do filho de Maria por um “quadradinho” e a idade de Maria, como é [tex]20[/tex] anos mais velha, por um “quadradinho mais [tex]20[/tex]”. Assim, montamos o seguinte esquema para distribuirmos os [tex]56[/tex] anos:
- A princípio, poderíamos pensar que teríamos que distribuir [tex]56[/tex] unidades entre os dois quadradinhos, mas perceba que [tex]20[/tex] das [tex]56[/tex] unidades a serem distribuídas já estão, digamos, comprometidas. Analisando o esquema acima, observamos que podemos descontar [tex]20[/tex] unidades das [tex]56[/tex] iniciais, [tex]56-20=36, \, [/tex] e dividir as unidades restantes entre os dois quadradinhos, [tex]36\div 2=18 \, [/tex].
- Pronto, esse resultado corresponde ao valor do quadradinho e obtemos as duas idades escrevendo:

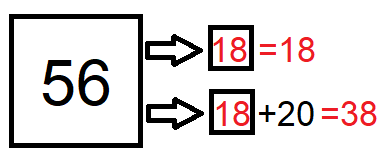
Logo, Maria tem atualmente [tex] \, \fcolorbox{black}{#eee0e5}{$38$} \, [/tex] anos.
Solução elaborada pelos Moderadores do Blog.
 |
Se você gostou da segunda forma de resolver o problema, conheça a Sala de Estudos Uma maneira diferente de resolver problemas do 1° grau.
|
