Problema
(Indicado a partir do 1º ano do E. M.)
Na imagem a seguir vemos o gráfico da função [tex]f:\mathbb{R}^+\rightarrow\mathbb{R}[/tex] definida por [tex]f(x)=log_{3}x[/tex].
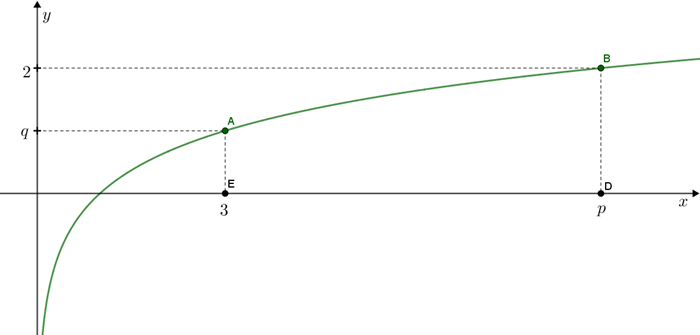
[tex]\textcolor{#800000}{(a)}[/tex] Quais os valores de [tex]p[/tex] e [tex]q[/tex] indicados no gráfico?
[tex]\textcolor{#800000}{(b)}[/tex] Calcule a área do trapézio [tex]ABDE \, [/tex], sabendo-se que os pontos [tex]A[/tex] e [tex]B[/tex] pertencem à curva definida por [tex]f[/tex] e os pontos [tex]D[/tex] e [tex]E[/tex] pertencem ao eixo [tex]x.[/tex]
[tex]\textcolor{#800000}{(c)}[/tex] Calcule os valores de [tex]x[/tex] tais que [tex]\left(f(x)\right)^2-7\left(f(x)\right)=-12.[/tex]
Solução
[tex]\textcolor{#800000}{(a)}[/tex] Como [tex]A[/tex] e [tex]B[/tex] são pontos da curva definida por [tex]f[/tex], então [tex]\boxed{f(3)=q} \, [/tex] e [tex]\boxed{f(p)=2} \, .[/tex]
Portanto, segue que:
- [tex]f(p)=2[/tex]
[tex] log_{3} p=2[/tex]
[tex] p=3^2[/tex]
[tex] \fcolorbox{black}{#eee0e5}{$ p=9$} \, .[/tex] - [tex]f(3)=q[/tex]
[tex] log_{3}3=q[/tex]
[tex] 3=3^q [/tex]
[tex] \fcolorbox{black}{#eee0e5}{$ q=1$} \, .[/tex]
[tex]\textcolor{#800000}{(b)}[/tex] Podemos observar que o trapézio [tex]ABDE[/tex] é um trapézio retângulo. Assim, fixada uma unidade de comprimento, podemos escolher o segmento [tex]\overline{BD} \, [/tex], cujo comprimento é [tex]2 \, [/tex], como sua base maior e o segmento [tex]\overline{AE} \, [/tex], cujo comprimento é [tex]1 \, [/tex], como sua base menor. Neste caso, a altura do trapézio seria o segmento [tex]\overline{ED} \, [/tex], cujo comprimento é [tex]9-3=6.[/tex]
Desta forma, a área, digamos [tex] S \, [/tex], do trapézio em questão é dada por:
[tex]\qquad \qquad \quad \fcolorbox{black}{#eee0e5}{$S=\dfrac{(2+1)\times 6}{2}=9$} [/tex] unidades de área.
[tex]\textcolor{#800000}{(c)}[/tex] Fazendo a mudança de variável [tex]y=f(x)[/tex] na equação [tex]\boxed{\left(f(x)\right)^2-7\left(f(x)\right)=-12} \, [/tex], encontramos a seguinte equação do segundo grau:
[tex]\qquad \boxed{y^2-7y+12=0} \, . \qquad \textcolor{#800000}{(i)}[/tex]
Para resolver a equação [tex]\textcolor{#800000}{(i)} \, [/tex], calculamos o discriminante, [tex]\Delta=1 \, [/tex], e já temos a certeza de que a equação possui duas raízes reais distintas. Aplicando a fórmula resolutiva de uma equação do segundo grau, [tex]y=\dfrac{-b\pm \sqrt{\Delta}}{2a}[/tex], obtemos as duas soluções dessa equação: [tex]\boxed{y_1=3} \, [/tex] e [tex]\boxed{y_2=4} \, .[/tex]
Mas [tex]y=f(x)[/tex]; assim, temos:
[tex]\hspace{2 cm} \begin{array}{ l | l }
y=3 \qquad &\qquad y=4\\
f(x)=3 \qquad &\qquad f(x)=4\\
log_3(x)=3\qquad &\qquad log_3(x)=4 \\
x=3^3\qquad &\qquad x=3^4 \\
x=27\qquad &\qquad x=81
\end{array} [/tex]
e, portanto, as soluções da equação [tex]\boxed{\left(f(x)\right)^2-7\left(f(x)\right)=-12}[/tex] são [tex] \, \fcolorbox{black}{#eee0e5}{$ x_1=27 \, \text{ e } x_2=81$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
