Problema
(Indicado a partir do 7º ano do E. F.)
Rob adora sorvete de chocolate. Quando foi ao supermercado com sua mãe, ele procurou de imediato o pote do seu sorvete favorito, mas infelizmente não encontrou. Decidiu, então, comprar dois potes de sorvete, ambos com mesmo volume. Um dos potes continha quantidades iguais dos sabores baunilha e chocolate, e o outro pote, quantidades iguais dos sabores chocolate, creme e morango.
Na compra, qual a fração de sorvete de chocolate adquirida?
Solução
Considere que [tex]\,c\,[/tex] é a capacidade de cada pote.
Deste modo, a fração de chocolate do primeiro pote é [tex]\,\dfrac{c}{2}\,[/tex] e do segundo pote, [tex]\,\dfrac{c}{3}[/tex].
Logo, a fração pedida é
[tex]\qquad \qquad \dfrac{\dfrac{c}{2}+\dfrac{c}{3}}{2c}=\dfrac{\dfrac{5c}{6}}{2c}=\dfrac{5c}{6} \times\dfrac{1}{2c}=\boxed{\dfrac{5}{12}}[/tex].
A figura abaixo ilustra a solução e a resposta do problema.
Lembre-se de que [tex]\;\dfrac{1}{2}=\dfrac{3}{6}\;[/tex] e [tex]\;\dfrac{1}{3}=\dfrac{2}{6}.[/tex]
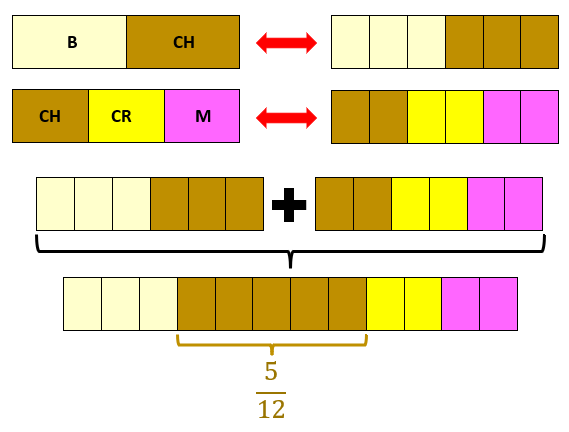
Solução elaborada pelos Moderadores do Blog.
Participou da discussão o Clube MIRIM APRENDIZ.
