Problema
(Indicado a partir do 2º ano do E. M.)
Dois cilindros circulares retos têm o mesmo volume. O raio do segundo cilindro é [tex]10 \%[/tex] maior do que o raio do primeiro.
Qual a relação entre as alturas dos dois cilindros?
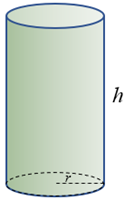
Lembrete
✐ Volume de um cilindro circular reto cujo comprimento da altura é [tex]h[/tex] e o comprimento do raio da base é [tex]r[/tex]:
[tex]\qquad \qquad \boxed{Volume=\pi\,r^2 h}.[/tex]
Solução
Sejam [tex]r_1[/tex] e [tex]r_2[/tex] os raios do primeiro e segundo cilindros, respectivamente. Da mesma forma, sejam [tex]h_1[/tex] e [tex]h_2[/tex] as alturas dos cilindros em questão. Assim, temos que
[tex]\qquad r_2=r_1+\dfrac{10}{100}\,r_1\\
\qquad r_2=\dfrac{11}{10}\,r_1\qquad \qquad (I) [/tex]
e
[tex]\qquad \pi\, r_1^2\,h_1=\pi\, r_2^2\,h_2.\qquad \qquad (II)[/tex]
De [tex] (I) [/tex] e [tex] (II) [/tex], segue que
[tex]\qquad r_1^2\,h_1=\dfrac{121}{100}\,r_1^2\,h_2 [/tex],
donde
[tex] \qquad h_1=\dfrac{121}{100}\,h_2=h_2+\dfrac{21}{100}\,h_2[/tex].
Portanto, a altura do primeiro cilindro é [tex] \,\fcolorbox{black}{#eee0e5}{$\,21 \%$}\,[/tex] maior do que a altura do segundo.
Solução elaborada pelos Moderadores do Blog.
